Marian Smoluchowski
Marian Smoluchowski (1872-1917)

Marian Smoluchowski (1872-1917)
W bieżącym roku mija 125. rocznica urodzin i 80. rocznica śmierci Mariana Smoluchowskiego [1]. Urodzony 28 maja 1872 r. w Vorderbrühl koło Wiednia, jako syn wyższego urzędnika kancelarii cesarskiej, Marian Smoluchowski studiował w latach 1890-1894 fizykę w Uniwersytecie Wiedeńskim, po czym w ciągu kilku lat zwiedził szereg najsłynniejszych ówczesnych ośrodków fizyki. Pracował w Paryżu pod kierunkiem Gabriela Lippmanna, w Glasgow pod kierunkiem Lorda Kelvina i w Berlinie u Emila Warburga. Pobyt u Warburga wywarł decydujący wpływ na przyszłą działalność naukową Smoluchowskiego, gdyż skierował jego uwagę na zagadnienia kinetycznej teorii materii.
Urodzony 28 maja 1872 r. w Vorderbrühl koło Wiednia, jako syn wyższego urzędnika kancelarii cesarskiej, Marian Smoluchowski studiował w latach 1890-1894 fizykę w Uniwersytecie Wiedeńskim, po czym w ciągu kilku lat zwiedził szereg najsłynniejszych ówczesnych ośrodków fizyki. Pracował w Paryżu pod kierunkiem Gabriela Lippmanna, w Glasgow pod kierunkiem Lorda Kelvina i w Berlinie u Emila Warburga. Pobyt u Warburga wywarł decydujący wpływ na przyszłą działalność naukową Smoluchowskiego, gdyż skierował jego uwagę na zagadnienia kinetycznej teorii materii.
Po habilitacji w 1898 r. w Wiedniu Smoluchowski objął w wieku 28 lat katedrę fizyki teoretycznej w Uniwersytecie Lwowskim (w 1899 r.). W rok później otrzymał nominację na profesora nadzwyczajnego, a w 1903 r. na profesora zwyczajnego. W 1913 r. przeniósł się ze Lwowa do Krakowa i objął katedrę fizyki doświadczalnej Uniwersytetu Jagiellońskiego. W 1917 r. został wybrany rektorem tegoż Uniwersytetu, lecz zanim zdołał objąć tę godność, zmarł 5 września tegoż roku w czasie epidemii dyzenterii.
Działalność naukowa Smoluchowskiego obejmowała wiele dziedzin fizyki. Najważniejsze jego osiągnięcia dotyczyły kinetycznej teorii materii. Jego prace miały przełomowe znaczenie dla rozwoju teorii atomistycznej i przyczyniły się w istotny sposób do rozstrzygnięcia sporu między zwolennikami a przeciwnikami teorii atomistycznej na korzyść atomistów.
Rozwój termodynamiki i kinetycznej teorii materii w ostatnich dziesięcioleciach XIX wieku
Zarówno termodynamika, jak i teoria kinetyczna materii były intensywnie rozwijane od początków XIX wieku. Szczególne sukcesy, jakie odnosiła termodynamika, doprowadziły pod koniec tego wieku do powstania, głównie w Niemczech, tak zwanej szkoły energetyków. Jej zwolennicy, wspierani przez kierunek filozoficzny, zwany empiriokrytycyzmem, uznający tylko fakty wynikające z doświadczeń i uważający hipotezy, wykraczające poza bezpośrednie wnioski z doświadczeń, za metafizykę, zaprzeczali istnieniu atomów. Szkole tej przewodzili Wilhelm Ostwald i Ernst Mach. Ostwald napisał nawet podręcznik chemii, w którym nie użył ani razu słowa "atom".

Równolegle z termodynamiką rozwijano w XIX wieku kinetyczną teorię materii i mechanikę statystyczną. Jeden z głównych wyników tej ostatniej polegał na zastąpieniu kategorycznych stwierdzeń drugiej zasady termodynamiki, tj. prawa wzrostu entropii, przez stwierdzenie, że zjawiska, w których entropia wzrasta, odbywają się z prawdopodobieństwem bardzo bliskim jedności. Nie potrafiono jednak do końca XIX wieku wskazać zjawisk, dla których stwierdzenia termodynamiki i mechaniki statystycznej różniłyby się, co pozwoliłoby uznać, która z obu teorii jest zgodna z doświadczeniem. Dlatego kinetyczna teoria materii stała się w tych latach bardzo niepopularna.
Ludwig Boltzmann, który wówczas przewodził atomistom, napisał w 1898 r. we wstępie do drugiego tomu swoich Wykładów o teorii gazów [2], że celem napisania Wykładów było ocalenie wyników kinetycznej teorii gazów, tak aby nie musiano na nowo odkrywać tego, co już zostało zrobione, gdy ta teoria odzyska uznanie.
Boltzmann nie dożył powrotu kinetycznej teorii materii do nauki. Ponowne jej wprowadzenie do fizyki i do chemii i wykazanie, że atomy istnieją, było dziełem wielu fizyków i chemików.
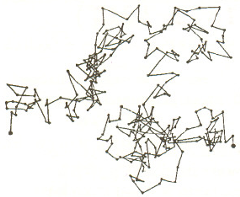
Ruchy Browna według obserwacji Perrina z 1908 r.
Najbardziej istotny udział mieli tu teoretycy: Albert Einstein i Marian Smoluchowski oraz eksperymentatorzy: Richard Zsigmondy, Theodor Svedberg i Jean Perrin. Zjawiska, pozwalające ustalić relacje między termodynamiką i teorią kinetyczną były już od dawna znane, lecz aby je prawidłowo objaśnić, potrzebny był geniusz Einsteina i Smoluchowskiego. Zjawiskami tymi były: ruchy Browna, opalescencja w stanie krytycznym i błękitny kolor nieba (później znaleziono ich więcej).
Ruchy Browna
Ruchy Browna polegają na nieustannym i nieregularnym przemieszczaniu się małych makroskopowo cząstek zawiesiny, "ziarenek", w ośrodku ciekłym lub gazowym. Te odkryte w 1827 r. ruchy badano przez cały wiek XIX tylko jakościowo. Wysuwano rozmaite przypuszczenia odnośnie przyczyn ich powstawania. Najczęściej sądzono, że:
- spowodowane były ruchami konwekcyjnymi w cieczy, wywołanymi przez nierównomierność temperatury,
- przyczyną ich były siły elektryczne, działające między ziarenkami,
- były wynikiem zderzeń ziarenek z nieregularnie poruszającymi się cząsteczkami ośrodka.
Pierwsze ilościowe doświadczenia nad ruchami Browna w pierwszych latach XX wieku wykonali: Felix Exner, Richard Zsigmondy i Theodor Svedberg. Wszyscy stwierdzili, że wykryte przez nich prawidłowości, rządzące ruchami Browna, były dla nich niezrozumiałe.
W latach 1905 i 1906 Einstein i Smoluchowski ogłosili niezależnie prace wyjaśniające w zupełności zjawisko ruchów Browna, opierając się na założeniu kinetycznej teorii materii, według której nieregularne ruchy ziarenek są spowodowane przez kolejne uderzenia cząsteczek ośrodka. Jako pierwsi zrozumieli, że obserwowane w doświadczeniach średnie przesunięcie ziarenka w sekundzie jest wielkością zupełnie inną, niż jego bardzo często zmieniająca się prawdziwa prędkość.

Praca Einsteina z 1905 r. nosiła tytuł O ruchu cząstek zawiesiny, postulowanym przez molekularno-kinetyczną teorię ciepła [6]. Einstein, stosując pojęcie ciśnienia osmotycznego i biorąc pod uwagę prawa mechaniki statystycznej obliczył średnie przesunięcie ziarenka w jednostce czasu. Lecz nie był pewny, jak to zaznaczył w swojej pracy, że badał rzeczywiście zjawisko ruchów Browna. Dopiero, gdy otrzymał dane doświadczalne, stwierdził w drugiej swojej pracy, ogłoszonej w 1906 r. pt. Przyczynek do teorii ruchów Browna [7], że jego teoria dotyczy właśnie tych ruchów.
Smoluchowski ogłosił pracę o ruchach Browna w 1906 r. Miała ona tytuł Zarys teorii kinetycznej ruchów Browna i roztworów mętnych [8]. Smoluchowski zajmował się zjawiskiem ruchów Browna od 1900 r. i pozostawał w kontakcie naukowym z Feliksem Exnerem. Wyników swoich badań nie ogłaszał, opublikował je dopiero po ukazaniu się pracy Einsteina. Metoda użyta przez Smoluchowskiego była całkiem inna niż metoda Einsteina. Smoluchowski świadomie rozpatrywał ruchy Browna. Średni kwadrat przesunięcia ziarenka w sekundzie obliczył badając szczegółowo mechanizm jego zderzeń z cząsteczkami ośrodka (dla uproszczenia rachunków rozważał ośrodek gazowy). Zdawał sobie sprawę z tego, że ruchy Browna są procesem stochastycznym (chociaż nie użył tego słowa), tak jak gry hazardowe lub błądzenie losowe. W omawianej pracy Smoluchowski porównał swoje wyniki z doświadczalnymi rezultatami Exnera i uzyskał dobrą zgodność. Powstaje więc pytanie, dlaczego nie opublikował swojej pracy wcześniej. Odpowiedź można znaleźć w atmosferze tamtych czasów, nieprzychylnej dla teorii kinetycznej. Ogłoszenie pracy z teorii kinetycznej było przeciwstawieniem się panującemu wówczas przekonaniu większości fizyków i dlatego Smoluchowski po sformułowaniu swojej teorii czekał na dalsze, bardziej wiarygodne wyniki doświadczalne.
Różnice między wynikami rachunków Einsteina i Smoluchowskiego były nieistotne, spowodowane przez przybliżenia, zastosowane przez Smoluchowskiego.

Wśród prac doświadczalnych, wykonanych zaraz po roku 1906, decydujące znaczenie miały prace Perrina, ogłoszone w 1908 r. Jego starannie wykonane pomiary dały niewątpliwą zgodność z przewidywaniami teorii Einsteina i Smoluchowskiego. Zgodność ta potwierdziła ostatecznie kinetyczne wytłumaczenie ruchów Browna i zadecydowała o uznaniu w nauce realnego istnienia atomów.
Ostwald, główny przeciwnik teorii atomowej, uznał w 1908 r. realne istnienie atomów.
Opalescencja w stanie krytycznym i błękit nieba
We wczesnych stadiach rozwoju kinetycznej teorii gazów uważano gaz za zbiór cząsteczek, mających jednakowe bezwzględne prędkości. Przyjmując to założenie Clausius wyprowadził równania stanu gazów doskonałych. Później Maxwell rozpatrywał gaz jako zbiór cząsteczek mających różne prędkości. Jednak uważano jeszcze gaz za zbiór cząsteczek, w którym gęstość jest stała. W pracy O nieregularnościach w rozkładzie cząsteczek gazu i ich wpływie na entropię i na równanie stanu [9], ogłoszonej w 1904 r., Smoluchowski pierwszy zwrócił uwagę na to, że gęstość gazu lub cieczy nie jest stała w całym obszarze przezeń zajmowanym, lecz ulega fluktuacjom. Polegają one na tym, że liczba 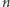 cząsteczek gazu lub cieczy w małej objętości
cząsteczek gazu lub cieczy w małej objętości 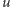 w zbiorniku o objętości
w zbiorniku o objętości 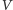 zmienia się z biegiem czasu, wahając się dokoła średniej liczby
zmienia się z biegiem czasu, wahając się dokoła średniej liczby 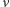 cząsteczek w objętości
cząsteczek w objętości 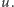 Zgęszczeniem liczby cząsteczek w objętości
Zgęszczeniem liczby cząsteczek w objętości  nazywamy wielkość
nazywamy wielkość

We wspomnianej pracy Smoluchowski obliczył średnie zgęszczenie cząsteczek w gazie doskonałym i otrzymał wartość

W następnej pracy o fluktuacjach pt. Teoria kinetyczna opalescencji gazów w stanie krytycznym oraz innych zjawisk pokrewnych [10] Smoluchowski obliczył w 1907 r. średnie zgęszczenie cząsteczek dla gazu van der Waalsa. Otrzymał przybliżoną wartość

gdzie 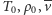 oznaczają kolejno: temperaturę bezwzględną, średnią gęstość cząsteczek i objętość właściwą gazu.
oznaczają kolejno: temperaturę bezwzględną, średnią gęstość cząsteczek i objętość właściwą gazu.
Pochodna 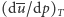 przyjmuje szczególnie duże wartości w pobliżu punktu krytycznego (gdzie
przyjmuje szczególnie duże wartości w pobliżu punktu krytycznego (gdzie 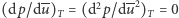 ), zatem tam fluktuacje są bardzo duże.
), zatem tam fluktuacje są bardzo duże.
Smoluchowski zwrócił uwagę na to, że fluktuacje powinny spowodować występowanie zjawisk charakterystycznych dla ośrodków mętnych, tj. zjawiska opalescencji oraz tzw. zjawiska Tyndalla, polegającego na rozpraszaniu promieniowania przechodzącego przez ośrodek mętny. W bliskości stanu krytycznego fluktuacje powodują powstanie opalescencji. Smoluchowski stwierdził też, że fluktuacje gęstości w powietrzu wywołują również lokalne zmiany współczynnika załamania i powodują przez to rozpraszanie światła w atmosferze. Ponieważ jest ono najsilniejsze dla fal krótkich, wynikiem przechodzenia światła dziennego przez atmosferę jest błękitny kolor nieba. Smoluchowski nie przeprowadził jednak obliczenia natężenia światła rozproszonego. Rachunki wykonał w 1910 r. Einstein w pracy pt. Teoria opalescencji cieczy jednorodnych i mieszanin w pobliżu stanu krytycznego [11] i otrzymał znany wzór Rayleigha.
Odwracalność i nieodwracalność
Zjawiska makroskopowe, podlegające prawom termodynamiki, są nieodwracalne, chociaż u ich podłoża tkwią odwracalne procesy molekularne, tego rodzaju jak zderzenia cząsteczek. Aby wyjaśnić, jak elementarne procesy odwracalne wywołują makroskopowe zjawiska nieodwracalne, Smoluchowski przeprowadził w latach 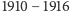 analizę doświadczeń Svedberga, polegających na kolejnych zliczeniach liczby ziarenek w ośrodku ciekłym w ograniczonym obszarze w polu widzenia ultramikroskopu, powtarzanych w jednakowych odstępach czasu. Analiza ta doprowadziła Smoluchowskiego do określenia "średniego czasu powrotu" [12]. Zdefiniujemy to pojęcie na przykładzie wspomnianych doświadczeń Svedberga. Dla określenia średniego czasu powrotu stanu, w którym w polu widzenia mikroskopu zaobserwowano
analizę doświadczeń Svedberga, polegających na kolejnych zliczeniach liczby ziarenek w ośrodku ciekłym w ograniczonym obszarze w polu widzenia ultramikroskopu, powtarzanych w jednakowych odstępach czasu. Analiza ta doprowadziła Smoluchowskiego do określenia "średniego czasu powrotu" [12]. Zdefiniujemy to pojęcie na przykładzie wspomnianych doświadczeń Svedberga. Dla określenia średniego czasu powrotu stanu, w którym w polu widzenia mikroskopu zaobserwowano 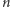 ziarenek, wyjdźmy od stanu, gdy zaobserwowaliśmy liczbę ziarenek różną od
ziarenek, wyjdźmy od stanu, gdy zaobserwowaliśmy liczbę ziarenek różną od 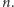 Załóżmy, że następnie obserwowaliśmy w równych odstępach czasu kolejno
Załóżmy, że następnie obserwowaliśmy w równych odstępach czasu kolejno 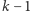 razy stany z liczbą ziarenek różną od
razy stany z liczbą ziarenek różną od 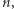 natomiast
natomiast 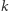 -ta obserwacja dała stan
-ta obserwacja dała stan 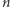 ziarenek. Jeżeli wykonamy wiele serii takich obserwacji, kończących się na stanie
ziarenek. Jeżeli wykonamy wiele serii takich obserwacji, kończących się na stanie 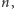 to średni czas trwania takiej serii nazwiemy średnim czasem powrotu i oznaczymy przez
to średni czas trwania takiej serii nazwiemy średnim czasem powrotu i oznaczymy przez 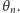 Z obliczeń Smoluchowskiego wynikło, że
Z obliczeń Smoluchowskiego wynikło, że

gdzie 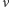 jest średnią liczbą ziarenek w polu widzenia ultramikroskopu, a
jest średnią liczbą ziarenek w polu widzenia ultramikroskopu, a 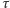 odstępem czasu upływającego między dwiema kolejnymi obserwacjami.
odstępem czasu upływającego między dwiema kolejnymi obserwacjami.
Zależność średniego czasu powrotu od liczby cząsteczek, biorących udział w procesie, ilustruje dobitnie przykład, podany przez Smoluchowskiego [13, 4].

Rozważmy małą objętość kulistą w powietrzu w warunkach normalnych. Okazuje się, że czas oczekiwania np. na pojawienie się fluktuacji stężenia tlenu na poziomie 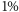 zależy bardzo silnie od promienia
zależy bardzo silnie od promienia  kuli, co widać z przytoczonej tabelki:
kuli, co widać z przytoczonej tabelki:
![|-------|------|-------|-------|--------|-------| |r-[cm]--|--1---|5⋅10−5-|3⋅10−5-|2,5-⋅10−5|1-⋅10−5-| |θ [sek] |101014 | 1068 | 106 | 1 | 10−11 | -------------------------------------------------](/math/temat/roznosci/historia_i_filozofia/2017/08/16/Marian_Smoluchowski/3x-53ee157f178de03c2a825451113dfdeb580e2d88-dm-33,33,33-FF,FF,FF.gif)
Dla większych kul, a więc dla większej liczby cząsteczek powietrza zjawisko jest praktycznie nieodwracalne, dla bardzo małych jest odwracalne.
Jako wniosek z rozważań tego rodzaju Smoluchowski wypowiedział kryterium odwracalności i nieodwracalności procesu: Zjawisko objawia się jako nieodwracalne (odwracalne), gdy średni czas powrotu stanu początkowego jest długi (krótki) w porównaniu z czasem obserwacji.
Uwagi końcowe
O ważności zagadnień badanych przez Smoluchowskiego i o ich roli w rozwoju nauki świadczy fakt, że trzech badaczy zajmujących się kinetyczną teorią materii, w tym dwóch współpracujących ze Smoluchowskim, zostało odznaczonych Nagrodą Nobla: Zsigmondy w 1925 r. i Svedberg w 1926 r. w dziedzinie chemii oraz Perrin w 1926 r. w dziedzinie fizyki.
Laureat Nagrody Nobla z 1983 r., Subrahmanyan Chandrasekhar wyraził opinię, że "... w serii prac, które Smoluchowski napisał w ciągu ostatnich pięciu lat życia, zostały położone podstawy nowoczesnej teorii procesów stochastycznych" [14].
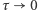 z uwzględnieniem szybkości wymiany cząsteczek przez powierzchnię kulki (dzięki czemu
z uwzględnieniem szybkości wymiany cząsteczek przez powierzchnię kulki (dzięki czemu 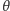 nie dąży do zera wraz z
nie dąży do zera wraz z  ).
).