Stabilnie czy dynamicznie?

Gdy w połowie XIX wieku w matematyce pojawiły się dziwne twory, w rodzaju funkcji ciągłych odcinka $[0; 1]$ na odcinek $|[0;1]$ w żadnym przedziale niemonotonicznych, czy zadań mających jednakowo poprawne, choć sprzeczne rozwiązania, jak paradoks Bertranda, potrzeba nadania matematyce jakiegoś jednoznacznego porządku, znalezienia odpowiedzi na pytanie, jak można, a jak nie należy matematyki uprawiać, stała się nagląca.

Paradoks Bertranda

Jakie jest prawdopodobieństwo, że losowo wybrana cięciwa okręgu ma długość nie mniejszą od boku trójkąta równobocznego wpisanego w ten okrąg?

I. Ponieważ każdy kierunek cięciwy jest jednakowo prawdopodobny, więc dla cięciw o ustalonym kierunku prawdopodobieństwo jest takie, jak dla wszystkich cięciw, czyli równe $|1~2.$

II. Ponieważ każdy koniec cięciwy jest jednakowo prawdopodobny, więc dla cięciw o ustalonym końcu prawdopodobieństwo jest takie, jak dla wszystkich cięciw, czyli równe $|1~3.$

III. Ponieważ każde położenie środka cięciwy jest jednakowo prawdopodobne, więc dla cięciw o ustalonym środku prawdopodobieństwo jest takie, jak dla wszystkich cięciw, czyli równe $|1~4.$

O kilku innych paradoksach rachunku prawdopodobieństwa można przeczytać w artykule Jacka Jakubowskiego opublikowanego w Delcie 4/1992.

Luka w Elementach

Rozwiązanie, które na ponad stulecie dominowało wśród matematyków, powstało w związku ze znalezieniem przez Moritza Pascha przesłanki, z której przez ponad dwa tysiące lat wszyscy uprawiający geometrię korzystali, a która nie wynika z postulatów zawartych w Elementach Euklidesa. Dziś przesłanka ta jest znana jako aksjomat Pascha i orzeka, że

Jeśli na płaszczyźnie prosta przecina jeden z boków trójkąta i nie przechodzi przez żaden wierzchołek, to przecina ona jeszcze jeden z boków (topologowie formułują to jako prosta rozcina płaszczyznę).

Pasch stwierdził, że owo korzystanie z niesformułowanego założenia dowodzi, iż matematycy często do przyjmowanych założeń dodają wiele swoich intuicji, i uznał, że matematykę należy od tego rodzaju dowolności uwolnić. Pierwszą przymiarkę do takiego doformułowania metodologii matematycznej zawarł w wydanym w 1882 roku Vorlesungen über neue Geometrie (Wykłady nowej geometrii), gdzie przedstawił uściśloną wersję Elementów.

Teoria formalna

Koncepcja Pascha trafiła na podatny grunt, a przez Hilberta została doprecyzowana i pod nazwą teoria formalna podniesiona do godności jedynie słusznego sposobu uprawiania matematyki. A wygląda to tak.

Jakieś znaczki, np. 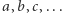$a, b,c,...$ nazywamy zmiennymi , wyróżniając wśród nich niektóre, np. 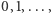$0,1,...,$ i zmyłkowo nazywając je stałymi.
Potem dołączamy do nich inne znaczki, funktory , np. 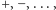$+,− ,...,$ wskazując przy tym ich sposób współżycia ze zmiennymi, np. 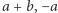$|a+ b,− a$ i nazywając tak zrodzone potomstwo termami oraz zalecając kazirodztwo, a więc traktowanie przez funktory termów jak zmienne, które dla niepoznaki od tego momentu też termami nazywamy.
Następnie dołączamy jeszcze inne znaczki, predykaty , np. 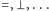$=, ,...$ również je instruując, jak mają sobie z termami poczynać, np. 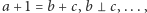$|a +1 = b + c,b c,...,$ tym razem potomstwo nazywając formułami elementarnymi.
Spójniki logiczne tworzą z nich formuły (już bezprzymiotnikowe).
Zbiór tak otrzymanych formuł to język.
Zdania rozmnażają się przez pączkowanie za pomocą operacji konsekwencji Cn.
Zbiór zdań, który już pączkować nie może, to właśnie teoria.

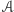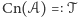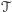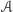Dla dowolnego zbioru zdań $𝒜$ oznaczmy przez $Cn( 𝒜) = 𝒯$ wszystko, co może z niego wypączkować. Dla tak otrzymanej teorii $𝒯$ zbiór $𝒜$ jest aksjomatyką.

Dawid Hilbert wierzył, że w taki sposób (ewentualnie "nieco" bardziej skomplikowany - teorie wyższych rzędów) da się opisać wszystko, czym zajmują się matematycy. Wierzył do tego stopnia, że nawet narzucił na przyzwoite teorie formalne dodatkowe wymagania.

Zażądał mianowicie (a może marzył o tym), by taka teoria była

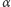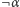niesprzeczna (z dwóch zdań $|α$ i $¬ α$ do teorii należy co najwyżej jedno);
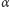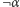zupełna (z dwóch zdań $α$ i $|¬α$ do teorii należy co najmniej jedno);
kategoryczna (wszystkie jej modele są izomorficzne, jednakowo zbudowane);
rozstrzygalna (istnieje skończona procedura sprawdzająca, czy dane zdanie do teorii należy).

Dziś wiemy, że żadna z interesujących matematyków dziedzin takiej aksjomatyki mieć nie może i starania nad jej poszukiwaniem dla przynajmniej niektórych dyscyplin zostały zarzucone w latach 70. ubiegłego stulecia. Jednak sam pomysł jest na tyle elegancki i przystający do specyfiki informatyki, że w jej ramach podobne problemy bada się nadal.

W matematyce w latach 30. XX wieku na taki sposób definiowania matematyki przypuszczono zdecydowany atak. Atak ten wykorzystał pomysł, którego precyzyjne sformułowanie było o 10 lat starsze od koncepcji Pascha.

Wieża Babel

Już w latach 30. XIX wieku Michel Chasles pisał:

Dziś każdy może przyjść, wziąć jakąkolwiek prawdę i poddać ją rozmaitym ogólnym zasadom przekształceń; otrzyma z niej nowe prawdy, inne lub ogólniejsze; i te poddać będzie można podobnym operacjom; w ten sposób możliwe będzie pomnożenie, prawie do nieskończoności, liczby nowych prawd, wyprowadzonych z pierwszej [...] nie musi już być geniuszem, kto chce dołożyć cegiełkę do gmachu geometrii.

Ta ponura opinia brała się stąd, że coraz bardziej zasadnie podejrzewano, że niektóre nowe teorie są tylko tłumaczeniem na inny język rzeczy znanych. Powstało zapotrzebowanie na sposób identyfikacji stwierdzeń różniących się jedynie formalizmem, w jakim są sformułowane.

Ale można było z możliwości posługiwania się różnymi formalizmami wyciągnąć pozytywne wnioski - przenoszenie rezultatów z jednej dziedziny do drugiej mogło pomagać w uprawianiu owej drugiej dziedziny. Duże wrażenie zrobił Übertragungsprinzip (ogólna zasada przenoszenia) Ludwiga Ottona Hessego. Hesse wskazał, że geometria rzutowa prostej (czyli prosta z homografiami) przez rzut stereograficzny da się przenieść na stożkową, a gdy znamy geometrię rzutową stożkowej, to możemy to rozciągnąć na jej wnętrze, a to już jest geometria płaszczyzny Bolyaia-Łobaczewskiego. To sformułowanie może wydawać się mętne nawet tym, którzy znają osobiście pojęcia występujące w poprzednim zdaniu. Wszelako na wielu matematykach zrobiło ono wielkie wrażenie. Julius Plücker w swoim Neue Geometrie des Raumes gegründet auf die Betrachtung der Geraden Linie als Raumelement (Nowa geometria przestrzeni, w której proste są rozważane jako elementy) swobodnie wskazywał, że proste przestrzeni trójwymiarowej tworzą rozmaitość czterowymiarową, ale mogą też być potraktowane jak sześciowymiarowa kwadryka, a więc siedmiowymiarowa geometria Bolyaia-Łobaczewskiego.

Te wszystkie oszałamiające hiperbole intelektualne zostały sprowadzone na ziemię przez ucznia Plückera, Felixa Kleina.

Na Marginesie

Program erlangeński wedle kursu geometrii analitycznej AD 1958

Grupy przekształceń $ℝn$ uporządkowane przez relację zawierania tworzą kratę. Ma ona element najmniejszy - grupę trywialną $| Id ,$ i element największy - grupę bijekcji. Można się temu przyglądać np. dla naturalnego dla nas $|n 3.$

Oznaczmy niezmienniki grupy $|G$ przez $G. |N$ Gdy zachodzi $1bG2, |G$ mamy $GcNG.N 12$ Zatem geometria (traktowana po kleinowsku) wyznaczona przez grupę $1 |G$ jest bardziej szczegółowa od geometrii wyznaczonej przez grupę $2, |G$ ma więcej pojęć i więcej twierdzeń. Np. geometrią wyznaczoną przez grupę trywialną posługują się w swych pracach geografowie. Inżynierowie używają geometrii bardziej szczegółowej od geometrii wyznaczonej przez grupę izometrii, gdyż śrubka lewoskrętna jest izometryczna (przystająca) do śrubki prawoskrętnej, a zamienić ich przy montażu się nie da. Nie bardzo wiadomo, kto miałby się posługiwać geometrią daną przez grupę izometrii. Wiadomo natomiast, kto posługuje się geometrią daną przez grupę podobieństw - takiej geometrii uczy się w szkole (patrz przytoczony przykład kwadratu czy koła). Pojęcia takie, jak graniastosłup czy ostrosłup, pojawiają się już w geometrii afinicznej (przekształcenia afiniczne to te bijekcje, które zachowują proste). Tamże mamy już twierdzenia Menelaosa i Cevy.

Warto zwrócić uwagę na fakt, że istotnie jest to krata, a nie porządek liniowy. Geometria dana przez podobieństwa i geometria dana przez grupę generowaną przez symetrie skośne nie są porównywalne: pierwsza z nich nie zachowuje objętości figur, a druga zachowuje. Z kolei pierwsza zachowuje kąty, a druga nie. Ich grupy automorfizmów nie są więc połączone relacją zawierania, ale obie zawiera grupa przekształceń afinicznych (te zachowują stosunek objętości, jak i one) i obie zawierają grupę izometrii.
(Objaśnienie: symetria skośna dana jest przez płaszczyznę $π$ i nierównoległą do niej prostą $|K$ w następujący sposób: przez punkt $P |$ i jego obraz $P$ przechodzi prosta równoległa do $|k,$ a środek $PP$ leży na $|π$ ; gdy $K π,$ otrzymujemy zwykłą symetrię).

Wadą takiego zredukowanego podejścia jest możliwość rozpatrywania tylko teorii operujących na tym samym zbiorze, co w przypadku prób pisania o związku geometrii afinicznej i rzutowej na ogół wówczas prowadziło, delikatnie mówiąc, do nieścisłości.

Program Erlangeński

Dwudziestotrzyletni Felix Klein, obejmując w 1872 roku katedrę matematyki w Erlangen, sformułował program badawczy, którego główna myśl polegała na tym, że dwa obiekty matematyczne należy uważać za tożsame, gdy mają tę samą grupę automorfizmów, co oznacza, że przekształcenia, które przeprowadzają te obiekty na nie same, mają takie same własności.

Jest to rewolucyjna zmiana sposobu patrzenia. Nie interesuje nas "z czego" jest zbudowany nasz obiekt, a jedynie to, jak może się sam na siebie przekształcać. Odpowiednikami twierdzeń, czyli elementów teorii formalnej, w ujęciu Kleina są własności niezmienników, czyli tych obiektów, które podczas przekształceń z grupy automorfizmów pozostają niezmienne.

Przykładem niezmienników mogą być znane figury: kwadrat, koło, które nie zmieniają się podczas podobieństw (tak! - kwadrat przy podobieństwie pozostaje kwadratem, a koło kołem).

Od razu widać potencjalną przewagę metody Kleina nad teorią formalną: zarówno niezmienników, jak też ich własności może być nieprzeliczalnie wiele, podczas gdy teoria formalna ledwie się do przeliczalności zbliża (znów odsyłam do wspomnianego na marginesie artykułu w Delcie 10/2016).

Ale tym, co jeszcze mocniej zaważyło na sukcesach tego podejścia, była możliwość uzyskiwania "za frajer" twierdzeń jakiejś teorii, gdy istniały stosowne twierdzenia teorii innej.

Oto dwa przykłady prac pokazujących natychmiast uzyskane tego rodzaju zyski.

Felix Klein, Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen von füften Gerade (Wykłady o dwudziestościanie i rozwiązywaniu równań piątego stopnia)
Sophus Lie, Über Complexe, inbesonders Linien und Kugelcomplexe, mit Anwendungen auf die Theorie partielle Differentialgleichungen (O liczbach zespolonych, a w szczególności prostych i stożkach zespolonych, z ich zastosowaniem w teorii równań różniczkowych cząstkowych)

Rysujące się tutaj możliwości były wykorzystywane jednak tylko przez nieliczną grupę matematyków. Na przykład ja, zaczynając studia 58 lat temu, byłem z pomysłem Kleina zapoznawany jedynie poprzez jego zastosowanie do klasyfikacji różnych geometrii zwykłej płaszczyzny, o czym piszę na marginesie.

Ale tak było do czasu.

Rewolucja bourbakistowska

Pewnego dnia w obfitującym w wydarzenia nie tylko matematyczne 1933 roku na Sorbonie wykład wygłosił nieznany i zamaskowany jakoby-profesor Nicolas Bourbaki i wezwał światową społeczność matematyczną do porzucenia skostniałej matematyki wywodzącej się z metody aksjomatycznej i bazującej na inspiracjach zaczerpywanych z fizyki. W zamian proponował dostrzeżenie, iż znakomite rezultaty uzyskujemy, obserwując dynamiczne zmiany, bo modyfikacja obserwowanych obiektów dostarcza nam więcej o nich informacji, tak, jak obserwacja pędzących rumaków więcej o nich nam powie niż wizyta w stajni.

Grupa matematyków ukrywająca się zbiorowo pod pseudonimem Bourbaki zaproponowała przeredagowanie matematyki na kleinowski sposób, publikując ponad 40 monografii obejmujących prawie wszystkie dziedziny matematyki. Członkowie zaś tej grupy swoimi wynikami dokumentowali, iż obrana przez nich metoda przynosi obfite owoce.

Jednak przeredagowywanie matematyki to robota niebagatelna i napotykająca wiele oporów. Spory na temat tego, w którą stronę matematykę poprowadzić, były bardzo ostre, niemal krwawe. W Polsce przesilenie nastąpiło w latach 60. XX wieku. Bourbakizm zwyciężył i dziś, gdy minęło już pół wieku, ślady po tej konfrontacji można odkryć, porównując programy studiów z moich czasów z dzisiejszymi.

Ewentualnych archeologów zainteresowanych problemem mogę odesłać do wtórnej książki Nicolasa Bourbakiego Elementy historii matematyki, gdzie hejtu na formalistów nazbierane jest niemało (ale ja tego cytować nie będę, bo to rzecz obrzydliwa, zwłaszcza u ludzi stwarzających podejrzenie, że intelekt mają niezerowy).

Istnieje, oczywiście, także teoria obsługująca technikę kleinowską, tak jak logika obsługiwała (a w informatyce nadal obsługuje) formalizm. To stworzona przez Samuela Eilenberga i Saundersa Mac Laine'a teoria kategorii, badająca obiekty i ich morfizmy, cokolwiek by to oznaczało.

Ale sukcesów dynamicznej metodzie badań matematycznych odmówić nie sposób: choćby klasyfikacja rozmaitości Grigorija Perelmana powstała z badań nad ich transformacjami w potokach Ricciego.