Tako rzecze Arystoteles

W -V wieku Parmenides stworzył szkołę filozoficzną, która postawiła sobie za cel zbadanie, jak ma się rozpowszechniona w tamtych czasach opinia, iż matematyka głosi najgłębszą prawdę o świecie, do rzeczywistości. Bez trudu dało się bowiem zauważyć, że pojęcia matematyki – taka, na przykład, prosta, albo – jeszcze bardziej – punkt, nijakich materialnych odpowiedników nie mają. Obiekt materialny można dzielić na mniejsze kawałki, ale przecież w końcu gdzieś będziemy musieli się zatrzymać, choćby z tego powodu, że nie można w skończonym czasie wykonać nieskończenie wielu czynności. Tymczasem matematyka pozwala choćby na odcinanie od odcinka stale połowy tego, co jeszcze zostało do dyspozycji, bez końca, a nawet pozwala stwierdzić, że w końcu z tego odcinka nic nie zostanie, nawet koniec.

Uczniowie Parmenidesa, zwani eleatami (od miejscowości w Italii, gdzie nauczał), ułożyli szereg aporii, czyli trudności, zalecając matematykom, by się nad nimi zastanawiali i by dopiero po ich pokonaniu brali się za uprawianie swojej dyscypliny. Powszechnie znane są aporie Zenona.

Problem był natury bardziej filozoficznej niż matematycznej i takie też było od początku jego rozumienie. Chodziło mianowicie o to, czy matematyka, której używamy do opisu realnego świata, Natury, jak wolano mówić, musi (względnie powinna) mieć taką samą strukturę, jak to, co nią opisujemy.

Oczywistą odpowiedź, że nie, dał Arystoteles. Ale uznał, iż nie każda konstrukcja myślowa jest, jako element służebnej dla przyrodników matematyki, dopuszczalna.

W szczególności odniósł się do łatwego do wypowiedzenia, ale trudnego do zdefiniowania, terminu nieskończoność. Tu zauważył, że nieskończoność może oznaczać coś płynącego, jak czas, albo też coś stabilnego, jak zawartość skarbca. I uznał, że te nieskończoności w istocie nie mają ze sobą wiele, a może nawet nic, wspólnego.

Pierwszą z nich nazwał nieskończonością potencjalną, utożsamił ją z możliwością kontynuowania jakiegoś procesu bez końca. Za jej pomocą rozwiązał prawie wszystkie aporie Zenona i uznał, że jej poprawne używanie nie grozi wpadnięciem w sprzeczności.

Drugą zaś – dysponowanie w jednej chwili nieskończoną liczbą obiektów – nazwał nieskończonością aktualną i stosowania jej odradzał, a nawet zabraniał.

Matematycy przez dwa tysiące lat jego dyrektyw przestrzegali, co nie przeszkodziło im w zbudowaniu potężnego gmachu analizy matematycznej, nieskończonością wręcz naładowanego.

Wszelako znalazł się śmiałek, który zakaz Arystotelesa złamał. Georg Cantor w dziele Grundlagen einer allgemeinen Mannigfaltigkeitslehre (1883) stworzył teorię mnogości, która w sposób oczywisty głosiła istnienie i sensowność zbiorów nieskończonych. I to różnie nieskończonych.

Zerwanie jabłka z drzewa wiadomości dobrego i złego wygnało ludzi z raju. Tu było podobnie. Sam Cantor z przerażeniem stwierdził, że umie udowodnić twierdzenia, które, jego zdaniem, powinny być nieprawdziwe – na przykład, że odcinek ma tyle samo punktów, co kwadrat, i co sześcian. Wpędziło go to we wzmagającą się paranoję, bo tych twierdzeń, przeciw którym protestował, dowodził coraz więcej. Ale wywołane przez niego zło pleniło się bujnie, co matematykom przynosiło coraz więcej kompletnie nienormalnych obiektów do kontemplacji i badań, a zwykłych ludzi skazało na naukę o zbiorach już od zerówki.

A nie lepiej było mieć jedną nieskończoność, przyzwoitą 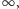$\text{[math]}$ i nie puszczać się na eksperymenty z różnymi kontinuami, alefami i innymi niestworzonymi dziwnościami?