Matematycy lubią zbiory nieskończone do tego stopnia, że wyróżniają zbiory mniej i bardziej nieskończone. Oto prosta konstrukcja myślowa. Dla danego zbioru 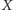 utwórzmy zbiór jego podzbiorów, 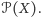 Na przykład dla 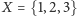 mamy osiem podzbiorów: pust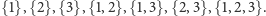y,  Gdy 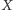 jest zbiorem skończonym o 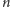  elementach, to 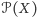 ma aż 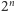 elementów. Matematycy robią z tego twierdzenie: nie ma odpowiedniości (tj. funkcji) wzajemnie jednoznacznej między elementami zbioru a wszystkimi jego podzbiorami i fakt, że 3 jest mniejsze od 8, uogólniają tak, by dał się zastosować do dowolnych zbiorów. Podzbiorów jest „bardzo więcej” niż elementów.

To twierdzenie dobrze działa na dusze matematyków – pokazuje im (tzn. nam) nieskończoną liczbę pięter nieskończoności, coraz obfitszych, coraz tłustszych, nie tak, jak chudziutkie 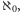 oznaczające najprostszą nieskończoność – tę, która jest udziałem ciągu liczb naturalnych

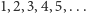
Równie ciepło myślimy o dowodzie, że liczb pierwszych jest nieskończenie wiele. Przypomnę. Gdyby liczb pierwszych było skończenie wiele, to ich iloczyn, powiększony o jedynkę, byłby... nową liczbą pierwszą, albo przynajmniej przez jakąś nową liczbę pierwszą by się dzielił.

W roku 2012 miałem semestralny wykład o matematyce dla wybranych studentów Instytutu Kultury Polskiej Uniwersytetu Warszawskiego. Instytut ma ambicje przyciągania najlepszych studentów, kształcących się w kierunkach humanistycznych. Nikt z nich, ale dosłownie nikt, nie zrozumiał tego dowodu nieskończoności zbioru liczb pierwszych, nie pojął, o co chodzi w tym przecież pięknym rozumowaniu. Bodaj najlepszy ze studentów, germanista, powiedział szczerze:

Poza problemem ontologicznym podnosił też pragmatyczny – przecież liczby w rodzaju 75295728956265922905722202572957 to nie jest rzeczywistość, to jeno nieodpowiedzialne konstrukcje myślowe, więc może jeśli nawet czegoś tam jest nieskończenie wiele, to te dalekie obiekty nie mają już znaczenia, można je zaniedbać.

Z refleksji nad tym, że bardzo wielkie liczby jawią nam się jako nieco inne twory, pojawiła się idea rozważania matematyki opartej na naszych aktualnych możliwościach poznawczych. W tej teorii operacje arytmetyczne nie są zawsze określone, bardzo wielkie liczby są „naturalne”, ale nie można ich interpretować jako zbiór jednostek (kropek, kresek, punktów, misiów pluszowych i tak dalej). Ponadto w zbiorze liczb „naturalnych” mogą być „luki” – nie wszystkie napisy to „naturalnie istniejące” liczby. Taki kierunek w podstawach matematyki nazywany jest aktualizmem. Zdecydowane próby stworzenia takiej matematyki podjął w latach sześćdziesiątych dwudziestego wieku Aleksandr Siergiejewicz Jesienin-Wołpin. Podważył on tak niewzruszone prawdy matematyczne, jak na przykład to, że operację „dodaj jeden” można stosować nieskończoną liczbę razy. Wszyscy bowiem wiemy, że następujące rozumowanie jest teoretycznie poprawne, ale... nic z tego nie wynika. Mianowicie można bez odpoczynku dojść piechotą z Lizbony do Białegostoku. Dowód:

Pierwszy krok oczywiście łatwo postawić. Jeżeli jednak postawię już dowolną liczbę kroków, to jeszcze jeden mały kroczek na pewno będę w stanie postawić.

Tego typu rozumowania właśnie próbował zanegować Jesienin-Wołpin. Kiedyś nie zdołamy tego kroku postawić.

Teoria Jesienina-Wołpina jest, owszem, ambitną próbą intelektualną, a jednak nie mamy wątpliwości, że jest udziwniona. Czy nie lepiej, np. zbierając grzyby, wierzyć, że ZAWSZE znajdzie się następny? Taką koncepcję nieustannego stawania się nazywamy nieskończonością potencjalną.

A przecież nieskończoności używamy też praktycznie, wierząc, że choćby woda ma strukturę ciągłą (bo inaczej, jak pływać?), mimo iż mędrcy wmawiają nam, że to zbiorowisko oddzielnych cząstek.

Nasze zmysły nie są cyfrowe, są analogowe – a zatem dopuszczają nieskończoną ilość stanów. Bez pojęcia nieskończoności bylibyśmy tak bezbronni jak komputery bez systemu operacyjnego, jak dzieci we mgle.

Nieskończoność. Cóż za pojęcie! Si non è vero, è ben trovato. Jeśli to nawet nie jest prawdziwe, to jednak dobrze wymyślone.

Tak, jak i cała matematyka...