Drobiazgi
Powiadają, że...
...dwaj najmłodsi uczniowie Galileusza, Bonaventura Cavalieri i Evangelista Torricelli, byli ludźmi do tego stopnia pogodnymi i pełnymi poczucia humoru, że nawet podczas pracy naukowej robili sobie wzajemnie zaawansowane psikusy ku uciesze znajomych.
Ich najważniejsze dzieło, Geometria indivisibilibus continuorum nova quadam ratione promota, przedstawiało oryginalną koncepcję powstawania podstawowych figur geometrycznych, nazwanych przez nich kontinuami. Twierdzili mianowicie, że linia to zapis dziejów punktu w jakimś przedziale czasu, powierzchnia to dzieje linii, a bryła to dzieje powierzchni. Przy takim podejściu istotne było podanie reguł, jak przy ruchu punktu powstaje długość, jak przy ruchu linii powstaje pole, a przy ruchu powierzchni – objętość.
Podobno w początkowej redakcji stosownego rozdziału Cavalieri napisał, że miary te są zsumowaniem elementów niższego wymiaru (tych tytułowych niepodzielnych): długość linii powstaje ze zsumowania punktów składających się na nią, pole – długości odcinków, a objętość ze zsumowania pól figur płaskich. Przeczytawszy to, Torricelli zaprosił znajomych na obiad, na którym stwierdził:
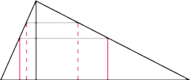
Mój kolega Bonaventura, oglądając (załączony) rysunek, udowodnił, że pole trójkąta prostokątnego z lewej strony jest równe polu trójkąta z prawej – przecież każdemu pionowemu odcinkowi składającemu się na jeden z nich odpowiada dokładnie jeden odcinek składający się na drugi!
Podobno koledzy śmiali się i bawili przez wiele godzin, a Cavalieri po powrocie do domu sformułował zasadę, nazywaną dziś jego imieniem, już poprawnie.