Początki geometrii przypominają malowidła naskalne (1), piramidy (2), wzory na wazach (3). Kształtem zaskakują dalsze znaczki - figury geometryczne (4,5,6,7). Większość znaczków to jednak prostokąty - niekiedy złote. Pierwszy trójkąt wszedł do obiegu pocztowego w 1853 r - widzimy go na znaczku Poczty RPA (8) (znaczek na znaczku) wydanym w 100-lecie jego urodzin. Znaczek z datownikiem okolicznościowym (9) prezentuje platońską koncepcję połączenia czterech żywiołów (Die vier Elemente - znaczek) z wielościanami foremnymi (datownik): czworościan - ogień, sześcian - ziemia, ośmiościan - powietrze, dwudziestościan - woda (odkryty później dwunastościan połączono z duchem). 2000 lat później Johannes Kepler połączył w tzw. kubku kosmograficznym wielościany foremne ze znanymi mu 6. planetami (10).

Znaczki to nie tylko figury geometryczne, ale także ich własności. Można więc odkryć (!) izometrie (11, 12, 13), (14) - taki współdruk filateliści nazywają tetbeszką, jednokładność (15) - na dolnym marginesie czytamy Arystarcha twierdzenie oraz podobieństwo (16), (17) - plan labiryntu w Knossos ulokowany na rewersie greckiej monety z - III w.! Moneta z czasów Euklidesa (17) jak najbardziej sprzyja stwierdzeniu, że to nie nić Ariadny wyprowadziła mitycznego Tezeusza z labiryntu, bo

W istocie, owa nić był to rysunek wykonywany na tarczy, a czasem i na dłoni

Marek Kordos, Wykłady z historii matematyki

Jest twierdzenie Pitagorasa (18, 19), (20) - to matematyka, chemia i fizyka (!) oraz twierdzenie Eulera (21). Niestety, na znaczku z Talesem (22) nie ma jego kluczowego dla podobieństwa twierdzenia - jest tylko bursztyn (elektron, j.gr.) przyciągający piórko! Szkoda!

Jest konstrukcja złotego podziału odcinka (23) (patrz Delta 11/2013) i przyrządy (24).

Są także liczby 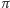(25) i 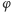(26, 27, 28). Anno Archimedeco ma tło zapisane cyframi rozwinięcia dziesiętnego liczby - jej ślad widzimy na datowniku okolicznościowym 21 - 3.14, co czytamy 21.03.14! Seria Poczty Liechtensteinu (złote prostokąty!) to skrócony życiorys liczby 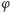- ciąg Fibonacciego, iloraz jego sąsiednich wyrazów, 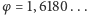- ozłocony datownikiem z kołowym fragmentem rozwinięcia dziesiętnego liczby 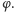Dodatkowo jeszcze dostrzegamy na (25) konstrukcje Archimedesa (górna pokazuje metodę wyczerpywania) oraz na (26, 27, 28) liść winogrona, jabłka, japońskiego klona - w tle ich rekonstrukcje z pomocą spiralnego rastra.

Porządek aksjomatyczno-dedukcyjny wśród figur i ich własności wprowadził Euklides (29) w Elementach (-300). Pierwsze definicje Elementów (30) - punkt, prosta - możemy odczytać w języku łacińskim na przywieszce znaczka z Collegium Maius. Próby dowodu V postulatu, poczynając od Proklosa (V w.), z czasem doprowadziły do uproszczenia jego zapisu i pojawienia się... geometrii nieeuklidesowych! Z trójki Janós Bolyai (31), Carl Friedrich Gauss (32), Nikołaj Iwanowicz Łobaczewski (33), w starciu o pierwszeństwo odkrycia, najbardziej ucierpiał Bolyai - podkreśla to mroczność jego pokoju (34). Słowo Appendix (Dodatek) przypomina dołączenie pracy Janósa do książki jego ojca a rysunek - zaprzeczenie V postulatu Euklidesa (rysunek bardziej nadaje się do ulokowania na znaczku z…Łobaczewskim). Istnienie nieskończenie wielu geometrii nieeuklidesowych wykazał Bernard Riemann w pracy O hipotezach jakie leżą u podstaw geometrii - pracę wydał Hermann Helmholtz (35) wraz ze swoją O faktach, które leżą u podstaw geometrii (1868). Znaczek (35) przedstawia badania Helmholtza z teorii barw i przystosowania oka.

Znaczki (36, 37, 38) ukazują związki geometrii z innymi działami matematyki, a (39) to, że... Znaczenie geometrii podkreśla fakt, że tak nazywano matematykę aż do połowy XIX w. - upamiętnia to projektant znaczka z Evariste Galois (40) pisząc pod jego portretem revolutionnaire et geometre.