(Nie)prawdopodobne izotopy
Wyobraźmy sobie fabrykę cząsteczek składających się z dwóch atomów wodoru  Inżynier obsługujący skomplikowaną maszynerię zgłasza do magazynu zapotrzebowanie na dwa atomy wodoru, jednak okazuje się, że dostępne są dwa typy atomów wodoru...
Inżynier obsługujący skomplikowaną maszynerię zgłasza do magazynu zapotrzebowanie na dwa atomy wodoru, jednak okazuje się, że dostępne są dwa typy atomów wodoru...
Oznaczymy je jako 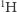 oraz
oraz 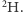 Różnią się one masą (dla typu
Różnią się one masą (dla typu 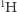 wynosi ona
wynosi ona 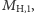 zaś dla typu
zaś dla typu 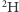 masa jest równa
masa jest równa 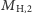 ). Dodatkowo, inżynier otrzymuje każdy z tych typów atomów wodoru z właściwym temu typowi prawdopodobieństwem (odpowiednio
). Dodatkowo, inżynier otrzymuje każdy z tych typów atomów wodoru z właściwym temu typowi prawdopodobieństwem (odpowiednio 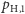 oraz
oraz 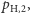 przy czym zachodzi równość
przy czym zachodzi równość 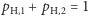 ).
).
W rezultacie teoretycznie ta sama cząsteczka 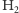 może być wyprodukowana w różnych odmianach. Załóżmy, że inżynier chciałby dowiedzieć się, którą cząsteczkę otrzymał, a jedynym narzędziem, które ma pod ręką, jest odpowiednio dokładna waga. Tak więc (pomijając kolejność atomów, która nie wpływa na masę) możliwe są trzy sytuacje:
może być wyprodukowana w różnych odmianach. Załóżmy, że inżynier chciałby dowiedzieć się, którą cząsteczkę otrzymał, a jedynym narzędziem, które ma pod ręką, jest odpowiednio dokładna waga. Tak więc (pomijając kolejność atomów, która nie wpływa na masę) możliwe są trzy sytuacje:
- (a)
- dwa atomy
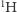 (o łącznej masie
(o łącznej masie 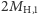 );
); - (b)
- jeden atom
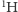 oraz jeden atom
oraz jeden atom 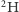 o łącznej masie
o łącznej masie 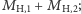
- (c)
- dwa atomy
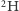 (o masie
(o masie 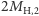 ).
).
Jeśli inżynier powtórzy swoje obserwacje dla dostatecznie dużej liczby cząsteczek, to częstości wystąpienia każdej z sytuacji (a), (b), oraz (c) będą odpowiadać prawdopodobieństwom wynoszącym odpowiednio 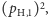
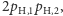 oraz
oraz 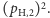 Warto podkreślić ciche dotąd założenie, że każdy z wodorów dostarczany jest niezależnie, więc prawdopodobieństwa się wymnażają; dwójka w wariancie (b) wiąże się z dwiema możliwymi konfiguracjami, których nie rozróżniamy w naszej analizie, tj.
Warto podkreślić ciche dotąd założenie, że każdy z wodorów dostarczany jest niezależnie, więc prawdopodobieństwa się wymnażają; dwójka w wariancie (b) wiąże się z dwiema możliwymi konfiguracjami, których nie rozróżniamy w naszej analizie, tj. 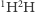 oraz
oraz 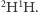
Jak się ma nasza wyobrażona sytuacja do rzeczywistości? Być może pamiętamy z lekcji chemii, że atomy (wbrew ich nazwie pochodzącej od greckiego słowa átomos, oznaczającego coś, czego nie da się już podzielić) składają się z jeszcze mniejszych cegiełek: protonów i neutronów (zwanych nukleonami, gdyż tworzą jądro atomowe) oraz dużo od nich lżejszych elektronów. Niektóre pierwiastki chemiczne mają swoje odmiany - izotopy - różniące się liczbą neutronów. W przypadku wodoru, podobnie jak w powyższej historyjce z inżynierem, obserwujemy dwie odmiany izotopowe: prot (jądro składa się z pojedynczego protonu) i deuter (w jądrze występuje jeden proton i jeden neutron), oznaczane właśnie jako 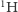 oraz
oraz 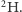 Występują one w danym środowisku w ustalonych proporcjach.
Występują one w danym środowisku w ustalonych proporcjach.
Dodajmy, że przy wyznaczaniu składników mieszanin można posłużyć się bardzo dokładną "wagą", tj. spektrometrem mas, który jest w stanie zbadać ilość substancji o zadanej masie. Bardziej precyzyjnie, spektrometr mas rozdziela cząsteczki względem wartości współczynnika 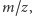 tj. stosunku masy do ładunku - mierzone są tylko naładowane cząsteczki; wartość
tj. stosunku masy do ładunku - mierzone są tylko naładowane cząsteczki; wartość 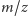 oblicza się np. na podstawie czasu, jaki potrzebuje cząsteczka na pokonanie określonej drogi w polu elektrycznym. My założymy dla uproszczenia, że nasz spektrometr mas analizuje cząsteczki naładowane znanym ładunkiem, więc przekształcenie między stosunkiem masy do ładunku a masą jest łatwe.
oblicza się np. na podstawie czasu, jaki potrzebuje cząsteczka na pokonanie określonej drogi w polu elektrycznym. My założymy dla uproszczenia, że nasz spektrometr mas analizuje cząsteczki naładowane znanym ładunkiem, więc przekształcenie między stosunkiem masy do ładunku a masą jest łatwe.
Podsumowując nasze dotychczasowe rozważania, cząsteczka wodoru 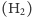 w idealnym eksperymencie będzie widoczna z grubsza w trzech różnych miejscach na osi oznaczającej masę. Masy protonu i neutronu są bardzo zbliżone. Dla uproszczenia załóżmy, że każdy nukleon waży jednostkę masy (oznaczoną jako dalton, Da), tak więc
w idealnym eksperymencie będzie widoczna z grubsza w trzech różnych miejscach na osi oznaczającej masę. Masy protonu i neutronu są bardzo zbliżone. Dla uproszczenia załóżmy, że każdy nukleon waży jednostkę masy (oznaczoną jako dalton, Da), tak więc 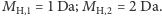 Przyjmijmy ponadto, że
Przyjmijmy ponadto, że 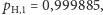 zaś
zaś 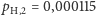 (użyte wartości odpowiadają w przybliżeniu rzeczywistym prawdopodobieństwom występowania poszczególnych izotopów w glebie wg standardu IUPAC, por. z tabelą na str. 7). Dla powyższych wartości możemy naszkicować rozkład prawdopodobieństw wariantów izotopowych wodoru względem ich masy (rysunek a). Od razu widzimy, że wyraźnie najbardziej prawdopodobny (ponad
(użyte wartości odpowiadają w przybliżeniu rzeczywistym prawdopodobieństwom występowania poszczególnych izotopów w glebie wg standardu IUPAC, por. z tabelą na str. 7). Dla powyższych wartości możemy naszkicować rozkład prawdopodobieństw wariantów izotopowych wodoru względem ich masy (rysunek a). Od razu widzimy, że wyraźnie najbardziej prawdopodobny (ponad 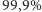 ) jest wariant najlżejszy.
) jest wariant najlżejszy.
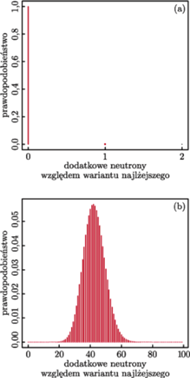
Rozkłady izotopowe cząsteczek (a) wodoru  oraz (b) surowiczej albuminy wołowej (BSA;
oraz (b) surowiczej albuminy wołowej (BSA; 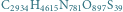 ).
).
Rozpatrzmy czysto hipotetyczną cząsteczkę wodoru składającą się z 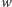 atomów (ozn.
atomów (ozn. 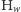 ). Teraz możliwe są następujące warianty izotopowe tej cząsteczki: dla
). Teraz możliwe są następujące warianty izotopowe tej cząsteczki: dla 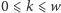 istnieje wariant składający się z
istnieje wariant składający się z 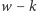 atomów
atomów 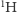 oraz
oraz 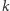 atomów
atomów 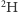 o masie
o masie 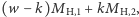 oraz o prawdopodobieństwie występowania:
oraz o prawdopodobieństwie występowania:
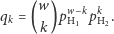 |
(1) |
Rozpoznajemy tu dobrze znany rozkład dwumianowy. Wprowadźmy wielomian 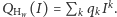 Zauważmy, że
Zauważmy, że 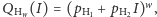 gdyż po wymnożeniu i zgrupowaniu wyrazów z
gdyż po wymnożeniu i zgrupowaniu wyrazów z 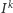 otrzymamy właśnie wartość prawdopodobieństwa wariantu o
otrzymamy właśnie wartość prawdopodobieństwa wariantu o 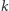 neutronów cięższego niż wariant najlżejszy. Funkcję
neutronów cięższego niż wariant najlżejszy. Funkcję 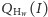 nazywamy funkcją tworzącą rozkładu cząsteczki
nazywamy funkcją tworzącą rozkładu cząsteczki 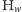 (z równania (1) znamy wzór na
(z równania (1) znamy wzór na 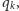 ale w bardziej skomplikowanych przypadkach funkcje tworzące okazują się bardzo wygodne). Ponadto, dla dużych
ale w bardziej skomplikowanych przypadkach funkcje tworzące okazują się bardzo wygodne). Ponadto, dla dużych 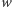 najbardziej prawdopodobny wcale niekoniecznie będzie wariant najlżejszy, np. dla
najbardziej prawdopodobny wcale niekoniecznie będzie wariant najlżejszy, np. dla 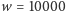 mamy
mamy 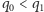 (sprawdzenie tej nierówności pozostawiamy Czytelnikowi jako proste ćwiczenie; ponadto proponujemy znalezienie najmniejszego takiego
(sprawdzenie tej nierówności pozostawiamy Czytelnikowi jako proste ćwiczenie; ponadto proponujemy znalezienie najmniejszego takiego 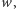 dla którego wskazana nierówność zachodzi). Powyższy przykład, choć wykorzystujący cząsteczkę hipotetyczną, miał na celu wyrobienie w Czytelniku intuicji, że nawet jeśli dla pojedynczego atomu wariant najlżejszy jest najbardziej prawdopodobny (w przypadku wodoru różnica wynosi kilka rzędów wielkości), to dla dużych cząsteczek wcale już niekoniecznie.
dla którego wskazana nierówność zachodzi). Powyższy przykład, choć wykorzystujący cząsteczkę hipotetyczną, miał na celu wyrobienie w Czytelniku intuicji, że nawet jeśli dla pojedynczego atomu wariant najlżejszy jest najbardziej prawdopodobny (w przypadku wodoru różnica wynosi kilka rzędów wielkości), to dla dużych cząsteczek wcale już niekoniecznie.
Rozważmy teraz cząsteczkę wody 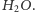 Tlen ma aż trzy stabilne izotopy, oznaczone jako
Tlen ma aż trzy stabilne izotopy, oznaczone jako 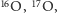 oraz
oraz 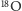 (wariant najlżejszy składa się z ośmiu protonów i ośmiu neutronów, kolejne warianty mają, odpowiednio, jeden i dwa neutrony więcej). Masy i prawdopodobieństwa poszczególnych izotopów dla rozważanych pierwiastków będziemy oznaczać analogicznie jak w przypadku wodoru. Tak więc w cząsteczce wody rozróżnimy pięć różnych wariantów izotopowych o prawdopodobieństwach:
(wariant najlżejszy składa się z ośmiu protonów i ośmiu neutronów, kolejne warianty mają, odpowiednio, jeden i dwa neutrony więcej). Masy i prawdopodobieństwa poszczególnych izotopów dla rozważanych pierwiastków będziemy oznaczać analogicznie jak w przypadku wodoru. Tak więc w cząsteczce wody rozróżnimy pięć różnych wariantów izotopowych o prawdopodobieństwach:
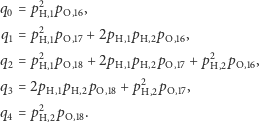
Widzimy, że powyższe wzory są już dużo bardziej skomplikowane. Dlatego raz jeszcze przyda się nam zastosowanie funkcji tworzącej, tym razem postaci 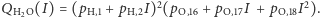 Poszczególne prawdopodobieństwa znów możemy uzyskać ze standardowej reprezentacji wielomianowej, tj.
Poszczególne prawdopodobieństwa znów możemy uzyskać ze standardowej reprezentacji wielomianowej, tj. 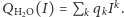

Badane w spektrometrii mas białka składają się głównie z pięciu pierwiastków chemicznych: wodoru, węgla, azotu, tlenu i siarki. Stabilne izotopy wraz z ich masami oraz prawdopodobieństwami występowania przedstawione są w tabelce obok. Dla związku chemicznego o sumarycznym wzorze 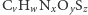 (
(  to liczba atomów węgla,
to liczba atomów węgla, 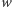 to liczba atomów wodoru itd.) odpowiednia funkcja tworząca ma postać
to liczba atomów wodoru itd.) odpowiednia funkcja tworząca ma postać
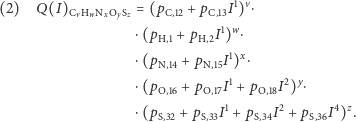
Warto zdawać sobie sprawę, że w przyrodzie występują białka o olbrzymiej liczbie atomów, np. surowicza albumina wołowa (oznaczana też BSA od ang. Bovine Serum Albumin) o wzorze chemicznym 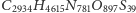 wcale nie należy do największych. Rozkład izotopowy tego białka prezentujemy na rysunku b. Rzeczywiście, mimo znacznej przewagi najlżejszych izotopów w przyrodzie, wariant najlżejszy przestaje być najbardziej prawdopodobny - dominuje natomiast wariant z
wcale nie należy do największych. Rozkład izotopowy tego białka prezentujemy na rysunku b. Rzeczywiście, mimo znacznej przewagi najlżejszych izotopów w przyrodzie, wariant najlżejszy przestaje być najbardziej prawdopodobny - dominuje natomiast wariant z 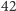 dodatkowymi neutronami. Tak więc dzięki obliczeniu teoretycznego rozkładu izotopowego łatwo zorientować się, że osoba analizująca BSA spektrometrem mas powinna oczekiwać, że aparat zmierzy substancję cięższą o około
dodatkowymi neutronami. Tak więc dzięki obliczeniu teoretycznego rozkładu izotopowego łatwo zorientować się, że osoba analizująca BSA spektrometrem mas powinna oczekiwać, że aparat zmierzy substancję cięższą o około 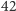 Da od masy najlżejszego wariantu tej cząsteczki.
Da od masy najlżejszego wariantu tej cząsteczki.
Często istnieje wiele cząsteczek o zadanej masie, każda dodatkowa informacja może więc być przydatna w poprawnej identyfikacji. Taką informacją jest, na przykład, właśnie rozkład izotopowy. Rozważmy dwie cząsteczki: propan 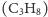 oraz dwutlenek węgla
oraz dwutlenek węgla 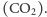 Mają one taką samą masę wariantu najlżejszego (
Mają one taką samą masę wariantu najlżejszego ( 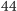 Da), w obu przypadkach też najwyższe jest prawdopodobieństwo tego wariantu. Gdy obliczymy stosunek prawdopodobieństw
Da), w obu przypadkach też najwyższe jest prawdopodobieństwo tego wariantu. Gdy obliczymy stosunek prawdopodobieństw 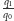 dla każdego z nich, okaże się, że choć obie wartości są bardzo małe, to jednak w przypadku pierwszej cząsteczki jest ona około trzy razy większa niż w przypadku drugiej (dokładne obliczenia pozostawiamy Czytelnikowi).
dla każdego z nich, okaże się, że choć obie wartości są bardzo małe, to jednak w przypadku pierwszej cząsteczki jest ona około trzy razy większa niż w przypadku drugiej (dokładne obliczenia pozostawiamy Czytelnikowi).
Przy przewidywaniu tego, jak będzie wyglądał dla danej cząsteczki wynik pomiaru w eksperymencie wykorzystującym spektrometr mas, pomocne może okazać się więc obliczenie jej rozkładu izotopowego. Problem ten sprowadziliśmy zaś do czysto matematycznego zagadnienia potęgowania wielomianów (por. równanie (2)). To już jednak temat na inną opowieść...
 oraz (b) surowiczej albuminy wołowej (BSA;
oraz (b) surowiczej albuminy wołowej (BSA; 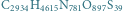 ).
).