Dźwięk to fala ciśnienia powietrza. Najprostsza, sinusoidalna fala jest charakteryzowana przez prędkość 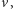 częstość 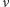(lub długość 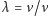) i amplitudę

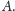
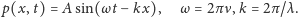(1)

Oczywiście, prawdziwe fale dźwiękowe, z którymi mamy do czynienia w życiu codziennym, mają bardziej skomplikowaną strukturę. Przedmioty emitujące dźwięki nie drgają z jedną konkretną częstością. Generowana przez nie fala jest raczej superpozycją, czyli złożeniem fal sinusoidalnych o różnych częstościach:

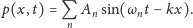(2)

Fale sinusoidalne są składnikami, które można łączyć w różnych proporcjach, uzyskując różne dźwięki. Od tego, w jaki sposób fale te poskładamy, zależy to, czy uzyskamy hałas, czy też ładny, „muzyczny” dźwięk. Odwrotnie, każdą falę można też rozłożyć na „czynniki pierwsze” zwane czasem modami, czyli wyznaczyć częstości i amplitudy fal sinusoidalnych, które ta fala zawiera.

Ponieważ energia drgań harmonicznych jest proporcjonalna do kwadratu amplitudy wychyleń, kwadraty amplitud fal sinusoidalnych o poszczególnych częstościach mówią nam, jaka energia zawarta jest w poszczególnych modach. Wykres zależności amplitud od częstości to tzw. widmo mocy.

Przykłady różnych widm mocy możemy obejrzeć na rysunkach 1 i 2. Nietrudno scharakteryzować różnice między nimi. Dźwięk helikoptera, który odbieramy jako hałas, zawiera w widmie mocy „gąszcz” składowych o prawie wszystkich możliwych częstościach, natomiast widmo mocy skrzypiec ma tych składowych niewiele i są one regularnie poukładane. Właśnie ta regularność widma odpowiada za to, że dźwięk skrzypiec „nadaje się” do tworzenia muzyki, czyli ma określoną wysokość. Widać wyraźnie, że dźwięk skrzypiec składa się z fal o częstościach będących wielokrotnościami pewnej częstości podstawowej (nazywamy je składowymi harmonicznymi). To właśnie częstość podstawowa decyduje o wysokości dźwięku.

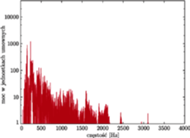
Rys. 1 Widmo mocy dźwięku helikoptera.

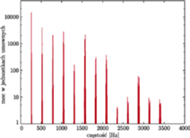
Rys. 2 Widmo mocy dźwięku skrzypiec.

Zastanówmy się przez chwilę, skąd bierze się takie widmo mocy. W strunie skrzypiec powstają fale stojące. Ponieważ struna nie może drgać na końcach, długość fali musi być taka, by wielokrotność połówki długości fali równała się długości struny. Długości fal w strunie o ustalonej długości to: 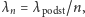 więc częstości to 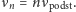 Pobudzając strunę do drgań, pobudzamy różne mody z różnymi amplitudami. To, jakie są amplitudy poszczególnych modów, decyduje o barwie dźwięku.

Uznaje się, że dobre współbrzmienia pojawiają się wtedy, gdy harmoniczne dwóch dźwięków w jakimś stopniu pokrywają się. Dzieje się tak, gdy stosunek częstości wynosi 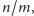 gdzie  i 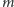  to względnie pierwsze liczby naturalne. Im mniejsza jest wspólna wielokrotność  i 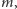  tym więcej wspólnych składowych mają te dźwięki.

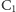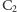W muzyce odległość między dźwiękami nazywamy interwałem. Fizycznie interwał jest po prostu stosunkiem częstości podstawowych dźwięków. Najprostszym interwałem jest oktawa. Odpowiada ona stosunkowi częstości  Oznacza to, że co druga harmoniczna danego dźwięku pokrywa się z harmoniczną dźwięku o oktawę wyższego (rysunek 3). Można więc powiedzieć, że jeśli zagramy te dwa dźwięki naraz (np.  i  ), uzyskamy dźwięk, który w zasadzie ma taką samą wysokość, jak dźwięk niższy, a różni się pełniejszym, bogatszym brzmieniem. Każdy dźwięk ma swój odpowiednik o oktawę wyższy, więc by stworzyć skalę, wystarczy poszukiwać dźwięków w ramach jednej oktawy, tzn. takich, które w stosunku do naszego wyjściowego C mają większą częstość, ale co najwyżej dwa razy.

W przypadku innych interwałów harmoniczne też mogą się w pewnej mierze pokrywać. Jeżeli zagramy dwa dźwięki o stosunku częstości podstawowych 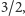 co trzecia harmoniczna dźwięku niższego będzie się pokrywać z co drugą harmoniczną dźwięku wyższego (rysunek 4).

Interwał odpowiadający stosunkowi częstości 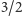 nazywamy kwintą. Kwinta w górę od 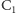 to dźwięk 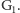 A jaka jest odległość między 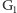 i 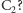  Można to wyliczyć, dzieląc stosunek częstości między 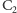 a 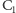  przez stosunek między 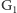 i 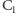 :  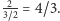Ten interwał nazywamy kwartą. Kwarta w górę od  to dźwięk, który nazywamy  Mamy więc stosunki częstości równe:  i 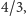  więc kolejnym może być 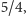 czyli tercja wielka (i oczywiście dopełniająca ją do oktawy seksta mała: ). 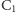Tercja wielka od  wyznacza nam 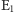(rysunek 4).

Kwinta i tercja wielka wystarczą, by zbudować podstawowy akord: trójdźwięk durowy, zawierający oba interwały. Akord C-dur składa się z dźwięków C-E-G. Trójdźwięk durowy to w pewnym sensie podstawowa „jakość” w harmonii. Co uzyskamy, jeżeli zbudujemy trójdźwięk durowy, zaczynając od 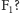 Dokładając do kwarty kwintę, mamy oktawę, a dokładając tercję, mamy nowy interwał – sekstę wielką 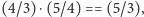 która wyznacza nam nowy dźwięk A. Akord F-dur składa się więc z dźwięków F-A-C. Z jakich dźwięków składa się w takim razie G-dur? Dokładając do kwinty 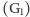 tercję wielką, mamy nowy interwał: septymę wielką 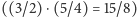 i dźwięk H. Dokładając kwintę, mamy 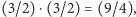 czyli więcej niż dwa. 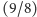Możemy jednak obniżyć ten dźwięk o oktawę i uzyskamy sekundę wielką  i dźwięk D. Akord G-dur zawiera więc dźwięki G-H-D.

Układając wszystkie dotychczas uzyskane przez nas dźwięki w kolejności rosnącej częstości, uzyskamy skalę C-dur: C-D-E-F-G-A-H-C, w której dźwięki pochodzą z trzech akordów: tzw. toniki C-dur, dominanty G-dur i subdominanty F-dur. Skala ta odpowiada białym klawiszom fortepianu.

Jaka jest odległość między drugim i trzecim dźwiękiem akordu durowego? Interwał ten nazywamy tercją małą, która (jak Czytelnik Wnikliwy może sprawdzić) odpowiada stosunkowi 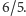 Akord, który zamiast tercji wielkiej ma tercję małą, to akord molowy. Prostym rachunkiem można pokazać, że z dźwięków skali C-dur można zbudować trzy akordy molowe: a-moll (A-C-E), d-moll (D-F-A) i e-moll (E-G-H).

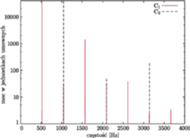
Rys. 3 Dwa dźwięki C w interwale oktawy.

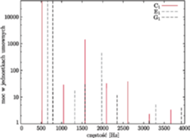
Rys. 4 Dźwięki tworzące akord C-dur: C-E-G.

Można sprawdzić, że próba zbudowania akordów molowych c-moll, f-moll i g-moll lub durowych A-dur, D-dur i E-dur, wyprowadza nas poza skalę. Dźwięki, które wtedy otrzymujemy, odpowiadają czarnym klawiszom fortepianu. W obrębie jednej oktawy mamy więc jedenaście dźwięków, których własności zebrane są w tabeli kończącej tekst.

Skalę durową można rozpocząć od dowolnego dźwięku. Napotykamy tu jednak niekiedy pewien problem. Opisane wyżej interwały to tak zwane interwały czyste. Jeżeli gramy na skrzypcach, które są instrumentem nietemperowanym, czyli umożliwiającym granie dźwięków o dowolnych częstościach, możemy je bez problemu zagrać, o ile mamy wystarczająco dobry słuch muzyczny. Na instrumentach temperowanych, np. na fortepianie, gramy „gotowe” dźwięki. Jest ich 11. Łatwo sprawdzić, że korzystając z tych dźwięków, nie da się zagrać czystej skali durowej, zaczynając od dowolnego dźwięku. Dla przykładu, drugi dźwięk w gamie D-dur powinien być o sekundę wielką wyższy od D, co daje stosunek 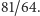 Takiej liczby w trzeciej kolumnie tabelki nie ma. 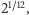Żeby na fortepianie móc grać w różnych tonacjach i żeby brzmiały one tak samo, opisane wyżej stosunki częstości, zwane strojem naturalnym, należy zastąpić strojem równomiernie temperowanym, w którym sekunda mała odpowiada stosunkowi częstości  a wszystkie interwały są jej złożeniami, czyli odpowiadają kolejnym potęgom tej liczby. Warto zauważyć, że w stroju równomiernie temperowanym składowe harmoniczne dźwięków są blisko siebie, ale już się nie pokrywają. Wydawać by się mogło, że akordy grane na fortepianie nigdy nie będą współbrzmieć. To „zepsucie” harmonii jest jednak nieznaczne: różnice między strojem czystym i temperowanym są na tyle małe, że słyszą je w zasadzie jedynie ludzie z kształconym słuchem. W czasach Bacha, kiedy budowano pierwsze „fortepianopodobne” instrumenty, w powszechnej opinii rzeczywiście strój równomiernie temperowany był uważany za szorstki i nieprzyjemny dla ucha. Dzisiaj jesteśmy otoczeni muzyką graną w tym stroju i brzmi ona dla większości z nas... naturalnie.