Galerię liczb nominałów otwierają ułamki (1) - (4) w zapisie na znaczkach rzadko dziś spotykanym. Do przeszłości natomiast należy już znaczek(5), na którym „przecinek” oddzielał 1 (szyling) od 6 (pensów) (1 szyling = 12 pensów – po reformie w 1971 r. pozostał tylko 1 funt szterling = 100 pensów). To samo powiemy też o znaczku (6) z nominałem 2 w zapisie arabskim (po lewej) oraz indyjskim (po prawej) wydanym w czasach wspólnoty Pakistanu Wschodniego (dziś niepodległy Bangladesz) i Zachodniego. Kolejne nominały 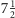(7) i 7+3 (8) wyróżnia ich arabski zapis od prawej do lewej. Wymownym dokumentem szalejącej 90 lat temu inflacji jest znaczek (9) z 50 000 000 000. opłatą! Dokumentem jest też blok (10) o nominale 2 000 forintów upamiętniający m.in. Światowy Rok Matematyki’2000 – wokół znaczka w ultrafiolecie można odczytać nazwiska 56-ciu węgierskich matematyków.

(1)	(2)	(3)	(4)	(5)
(6)	(7)	(8)	(9)	(10)

Dalsze okazy (11) – (19) są już normalne – podwójne nominały na większości z nich pozwalają porównać cyfry „inne” z „naszymi”. Urywek historii tych ostatnich (20) przypomina zachowany przez wieki Codex Vigilanusa(21) (Madryt, 976) oraz zegar słoneczny (22) (Praga, 1524) z cyframi na tarczy mającymi już, oprócz 4 i 7, dzisiejszy kształt.

(11)	(12)	(13)	(14)	(15)
(16)	(17)	(18)	(19)	(20)
(21)	(22)	(23)	(24)	(25)

Pora na liczby nie-nominały. Najstarsza z nich – Podziwu godna liczba Pi -(23) na najdłuższym łuku liczy ok. 90 cyfr. Jest też na znaczku (24) oraz bloku (25) z cyframi, które ustalił 1500 lat temu Cu Czung-czy. Szkoda, że nie ma  na znaczku z Archimedesem (26) – był jej „fanem”, ustalił wartość 22/7 oraz udowodnił m.in. że ma taką samą wartość we wzorach na długość okręgu i pole koła. „Kształt” poetycki nadała jej Wisława Szymborska w wierszu „Liczba Pi” – jego fragment własnoręcznie napisany przez autorkę można przeczytać na (27). 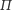 ma też swój zielony pomnik – skwer (3 miłorzęby i 14 krzaczków jałowca) przed wejściem do Wydziału Mat-Fiz-Chem Uniwersytetu Śląskiego przy ul. Augusta Chełkowskiego 3,14 (28). Jej święto obchodzimy 14 marca – na widokówce (29), wysłanej z Londynu w 1907r brakuje 3.14 za to są datowniki pocztowe 3.15 oraz 3.13 (MAR.13) (przybliżenia ).

(26)

(27)

(28)

(29)

(30)

Liczbę 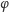 (30) dostrzegła, jako pierwsza, Poczta Związku Radzieckiego (1959) . 48 lat później Poczta Macao uhonorowała ją kolorowym, „rodzinnym” (!) blokiem (31) oraz czteroznaczkową serią (32). W centrum bloku, o wymiarach 135x85 (prawie złotych) znajduje się liczba 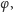 jej najbliżsi „krewni” widoczni są w rogach – konstrukcje złotego (boskiego) cięcia opisane numerkami oraz w tle cyfry jej rozwinięcia dziesiętnego (jest ich 4410). Dalsze, raczej niespodziewane „ pokrewieństwo” można podziwiać na znaczkach serii z tłem zapisanym także cyframi jej …Określenie boska proporcja wprowadził Luca Pacioli (33) w pracy „O boskiej proporcji” (1509) z ilustracjami Leonarda da Vinci (34) – na obrzeżu (33) znajduje się tytuł jego najważniejszego dzieła.

(31)

(32)

(33)

(34)

(35)

Skromną reprezentację ma liczba e – wzór Eulera (35), logarytm naturalny (36). Jest również zero (37), liczba ujemna (38) i liczba pierwsza Martina Mersenne’a (39).

(36)

(37)

(38)

(39)

(40)

Mamy też liczby z systemów różnych od „naszego”. Na przywieszce znaczka Izraela (40) widzimy po lewej 1960 r., zaś po prawej jego odpowiednik w kalendarzu żydowskim zapisany alfabetem liczbowym (akcent między literami oznacza, że nie jest to słowo lecz liczba). Za literami czytanymi od prawej do lewej kryją się 400, 300, 20, 1 – ich suma 721 z dopisanym 5, zgodnie z tzw. małą rachubą, daje rok 5721. Różnica 1960 – 5721 = -3761 to umowny pierwszy rok ery żydowskiej.

System Majów (podobny do 20-stkowego) liczy 20 cyfr. Muszla oznacza 0, odpowiedni układ kropek i kresek- 1, 2, 3, …19. Na znaczkach (41) - (43) łatwo dostrzec niektóre z nich, np. dwie kropki i kreska to 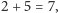 kropka i dwie kreski to 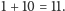 Liczby zapisywano w pionie – na dole jedności , potem dwudziestki i dalej 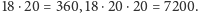 W kalendarzowych zapisach stosowano tzw. glify- na zabytkowym dysku (42), (43) (Chinkultic,591) majańskiego piłkarza otacza pierścień kołowy z datą cyfrowo-glifową [9.7.17.12.14] równą liczbie dni od początku majańskiej ery (11 sierpień 3114r p.n.e.):

(41)

(42)

(43)

(44)

(45)

Znaczki (44) i (45) przypominają systemy rzymski i binarny.

I na koniec niespodzianka – liczby urojone w nieurojonym obiegu pocztowym. Liczby zespolone (46) oglądamy na płaszczyźnie Gaussa (Arganda, Eulera, Wessela?) w interpretacji kolorowo-prostokątnej, zaś kwaterniony (dokładnie formuły mnożenia) (47) „czytamy” wyryte przez R.W. Hamiltona 16.10.1843 na poręczy mostu Brougham w Dublinie. Oba znaczki ukazały się w dwusetne urodziny Carla Friedricha Gaussa (1977) i Williama Rowana Hamiltona (2005).

(46)