Aktualności (nie tylko) fizyczne
Jak to działa?
(Nie)bezpieczne lądowanie
Do poturbowanego kolarza, który przed chwilą przeżył karambol, podchodzi dziennikarz i pyta: czy pan uprawia sport dla zdrowia czy dla przyjemności?
Sport wyczynowy to nie zabawa. Dotyczy to nie tylko dyscyplin olimpijskich. Szczególnie widoczne jest to w sportach ekstremalnych – „ekstremalne” jest to, czego nie byłby w stanie zrobić amator.
Przykładem może być jeżdżenie na nartach po…nienadających się do tego dziewiczych terenach. Jazda w głębokim śniegu po bardzo stromych stokach (dostępna dla zdolnego amatora) jest przerywana skokami z urwisk skalnych. Właśnie takie skoki czynią tę formę uprawiania narciarstwa dosłownie ekstremalną.
Pokrewną konkurencją stały się ewolucje na specjalnych skoczniach, tzw. skoki big air (nie należy ich mylić z olimpijską już konkurencją skoków akrobatycznych na jeszcze innej odmianie skoczni).
Choć w obu tych odmianach narciarstwa (i snowboardu) rozgrywane są zawody z mistrzostwami świata włącznie, to głównym zajęciem mistrzów tych konkurencji jest dostarczanie zdjęć do magazynów narciarskich (i snowboardowych).
W skokach typu big air przelatuje się od kilkunastu do kilkudziesięciu metrów, wznosząc się na wysokość kilku metrów i wykonując w locie salta, obroty lub jedno i drugie. Podobne ewolucje urozmaicają niektóre skoki ekstremalnej jazdy pozatrasowej. Na tylnej okładce pokazany jest przykład takiego przejazdu (niestety, niektóre ujęcia mogą być jednocześnie poglądową demonstracją zasady nieoznaczoności). Różnica wysokości przy drugim skoku wynosi około 10 metrów. Czy normalny człowiek może bez szkody dla zdrowia zeskoczyć z tak wysoka? Na zdjęciu widać zresztą, że narciarz nie ustał tego skoku. Czy tylko przypadkiem udało mu się wstać i pojechać dalej?
Na szczęście oprócz odwagi, sprawności i umiejętności miłośnicy białego (dosłownie) szaleństwa mają potężnego sprzymierzeńca – zasady fizyki.
Na szczęście oprócz odwagi, sprawności i umiejętności miłośnicy białego (dosłownie) szaleństwa mają potężnego sprzymierzeńca – zasady fizyki.
To, z jakiej wysokości można po skoku bezpiecznie wylądować, zależy
po pierwsze od tego, jak długa będzie droga hamowania. Przyjmijmy
najkorzystniejszy wariant hamowania ze stałym przyspieszeniem. Wtedy
przeciążenie wyraża się szczególnie prostym wzorem. Stosunek dodatkowego
przyspieszenia do przyspieszenia ziemskiego jest po prostu równy stosunkowi
wysokości skoku do długości drogi hamowania (wynika to z faktu, że praca
wykonywana przez przyspieszenie w ruchu jednostajnie przyspieszonym jest
równa iloczynowi masy, przyspieszenia i przebytej drogi). Jeżeli hamowanie
jest związane tylko z ugięciem nóg, to droga hamowania wynosi około pół
metra. Już przy skoku z wysokości 5 metrów przeciążenie wynosiłoby więc
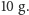 Przeciętny człowiek nie ma nóg mogących wytrzymać coś takiego
bez poważnej kontuzji. Dlatego nikt rozsądny nie wyskakuje z drugiego
piętra.
Przeciętny człowiek nie ma nóg mogących wytrzymać coś takiego
bez poważnej kontuzji. Dlatego nikt rozsądny nie wyskakuje z drugiego
piętra.
Czym różnią się skoki prezentowane na okładce od skoku z drugiego
piętra? Bo przecież nie wysokością. Po pierwsze, spada się na miękki śnieg.
Dzięki temu można uzyskać dodatkową drogę hamowania nawet rzędu metra.
W tym konkretnym przypadku zysk wynosi jednak tylko około 20 cm.
(Pokrywa świeżego śniegu nie jest głębsza niż wysokość butów
narciarskich), co i tak zmniejsza przeciążenie (przy pierwszym skoku) do około
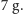 To, niestety, nadal sporo. Następne zmniejszenie przeciążenia jest
związane z lądowaniem na stromym stoku. Wyhamować trzeba tylko składową
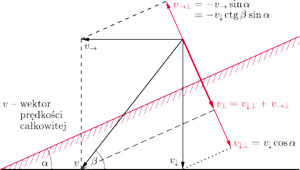
prędkości prostopadłą do stoku. Ponieważ prędkość we wzorze
na energię kinetyczną występuje w kwadracie, to pojawia się czynnik równy
kwadratowi kosinusa kąta nachylenia. Im większa stromizna, tym łagodniejsze
lądowanie! W sytuacji pierwszego skoku z okładki czynnik ten wynosi około
0,85. Ale to jeszcze nie koniec. Przecież narciarz ma pewną prędkość
poziomą, która ma składową prostopadłą do stoku skierowaną od stoku
w górę.
To, niestety, nadal sporo. Następne zmniejszenie przeciążenia jest
związane z lądowaniem na stromym stoku. Wyhamować trzeba tylko składową
prędkości prostopadłą do stoku. Ponieważ prędkość we wzorze
na energię kinetyczną występuje w kwadracie, to pojawia się czynnik równy
kwadratowi kosinusa kąta nachylenia. Im większa stromizna, tym łagodniejsze
lądowanie! W sytuacji pierwszego skoku z okładki czynnik ten wynosi około
0,85. Ale to jeszcze nie koniec. Przecież narciarz ma pewną prędkość
poziomą, która ma składową prostopadłą do stoku skierowaną od stoku
w górę.
Lądowanie bedzie tym łagodniejsze, im szybciej narciarz (poziomo) się porusza!
Czynnik
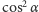 zmniejsza się więc i wynosi
zmniejsza się więc i wynosi
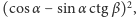 co
liczbowo, w sytuacji omawianego skoku, jest równe około 0,4. Ostatecznie
szacowane przeciążenie przy pierwszym skoku wyniosło tylko około
co
liczbowo, w sytuacji omawianego skoku, jest równe około 0,4. Ostatecznie
szacowane przeciążenie przy pierwszym skoku wyniosło tylko około
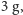 czyli było równoważne zwykłemu skokowi z około półtora metra, co nie
stanowi wielkiego wyczynu. Zauważmy, że na skoczni używanej do skoków
big air można tak dobrać prędkość najazdową, żeby wektor prędkości
całkowitej w momencie lądowania był prawie równoległy do zbocza,
praktycznie eliminując przeciążenie.
czyli było równoważne zwykłemu skokowi z około półtora metra, co nie
stanowi wielkiego wyczynu. Zauważmy, że na skoczni używanej do skoków
big air można tak dobrać prędkość najazdową, żeby wektor prędkości
całkowitej w momencie lądowania był prawie równoległy do zbocza,
praktycznie eliminując przeciążenie.

Zamiast rozpatrywać drugi skok z okładki (który został wykonany w kierunku kamery, co utrudnia szczegółową analizę), zajmijmy się skokiem przedstawionym na następnej stronie. Jest on naprawdę straceńczy. Wysokość pokonanego skokiem urwiska wynosi około 40 metrów! W dodatku narciarz ma bardzo małą prędkość poziomą. Stok jest co prawda bardzo stromy i pokryty grubą warstwą świeżego śniegu, ale skok zakończył się praktycznie całkowitym zatrzymaniem narciarza. Dopiero po zatrzymaniu wstał on i pojechał dalej, co dowodzi, że skok przeżył bez widocznego uszczerbku zdrowia. Ponowne lądowanie związane było z upadkiem na plecy. Czy taki upadek jest elementem techniki lądowania? Ze zdjęcia można odczytać, jaka była całkowita droga hamowania.

Jest to różnica wysokości środka masy (znajdującego się mniej więcej na wysokości biodra) w momencie pierwszego zetknięcia się nart ze śniegiem i domniemanego jego położenia w momencie zatrzymania (ten moment odpowiada ujęciu, na którym widać tylko wystające ze śniegu narty).
Stosowana przy takich skokach technika lądowania maksymalnie wydłuża tę drogę hamowania.
W pierwszej fazie wykorzystywana jest sprężystość nart, których tyły wyginają się przy zetknięciu ze śniegiem. Jednocześnie narty przebijają się przez warstwę śniegu, której efektywna grubość jest tym większa, im bardziej stromy jest stok. W końcu tyły nart dochodzą do twardego podłoża i w tym momencie narciarz pozwala, aby narty wyjechały spod niego. Dzięki temu zaczyna się zmieniać kierunek prędkości narciarza na równoległy do stoku, a narciarz może do wyhamowania użyć całego ciała zapadajacego się w świeżym śniegu, a nie tylko nóg. Jeżeli uda mu się rozpocząć dalszą jazdę bez zatrzymania (umiejętnie wykorzystując opór stawiany przez narty do powstania), to taki sposób lądowania odpowiada przeciążeniu związanemu tylko ze zmianą prędkości (która może być istotnie mniejsza od prędkości całkowitej). Jeżeli nie, to ostatnim hamulcem są nogi.
W sytuacji drugiego skoku przedstawionego na okładce maksymalne
przeciążenie można oszacować na około
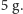 Natomiast
na przedstawionym tu skoku z 40 metrów, z drogą hamowania 4 metry, nadal
otrzymujemy oszacowanie na poziomie co najmniej
Natomiast
na przedstawionym tu skoku z 40 metrów, z drogą hamowania 4 metry, nadal
otrzymujemy oszacowanie na poziomie co najmniej
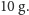
Czy jeszcze jakieś prawo fizyki może przyjść narciarzowi z pomocą? Powyższe oszacowanie zostało zrobione przy założeniu, że narciarz spada ruchem jednostajnie przyspieszonym. Sekwencję zdjęć (bogatszą niż tu przedstawiona) można wykorzystać do oszacowania zależności prędkości od czasu. Otrzymane punkty przedstawione są na rysunku, wraz z dopasowaną do pierwszych kilku zależnością liniową odpowiadającą ruchowi jednostajnie przyspieszonemu oraz dopasowaną do wszystkich punktów parabolą.
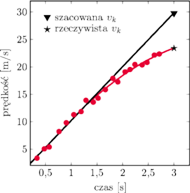
Pionowa składowa prędkości narciarza. Kolorowe punkty i poprowadzona przez nie linia odpowiadają rzeczywistości. Prosta czarna linia odpowiada zaniedbaniu oporu powietrza.
Z porównania obu dopasowań można wnioskować, że na skutek oporu
powietrza końcowa prędkość była o czynnik około 3/4 mniejsza, niż gdyby
ruch odbywał się ze stałym przyspieszeniem. W takim razie końcowa energia
kinetyczna była 9/16 razy mniejsza, czyli w poprzednim oszacowaniu
powinniśmy zmniejszyć wysokość skoku do 20–25 m. Otrzymalibyśmy
wtedy przeciążenie około
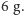
Wypada w tym momencie ostrzec, zwłaszcza młodych Czytelników. Z faktu, że nasze oszacowania przeciążeń są zadziwiająco niskie, nie wynika, iż omawiane ewolucje są bezpieczne. Po pierwsze, są to oszacowania dolnej granicy maksymalnego przeciążenia, które chwilowo może być dużo większe. Dowodzą one nie tego, że każdy taki skok można przeżyć, tylko tego, że jego przetrwanie nie tylko nie jest sprzeczne z prawami fizyki, ale że technika lądowania optymalnie te prawa wykorzystuje.
Na koniec można zrobić jeszcze jedną ciekawą obserwację dotyczącą drugiego skoku z okładki. Żeby lądowanie było optymalne, należy zetknąć się ze stokiem w odpowiedniej pozycji. Najczęstszym błędem przy skokach jest złe wybicie skutkujące pozycją zbyt wychyloną lub zbyt odchyloną. Robienie salta, co wygląda na dodatkową trudność, może pomóc. Moment bezwładności łatwo reguluje się poprzez stopień wyprostowania sylwetki, a tym samym wpływa się na tempo obrotu, co umożliwia kontrolę pozycji w momencie lądowania. Żeby tę możliwość wykorzystać, potrzebne jest jednak świetne wyczucie.
I na koniec uwaga dla miłośników narciarstwa. Tak, dobrze się domyślacie. W obu prezentowanych sekwencjach narciarskich używany był sprzęt telemarkowy: free your heel, free your mind (uwolnij piętę, uwolnij umysł).