Paradoksy dedukcji
Definicja paradoksu obejmuje różne sytuacje, powody i postacie paradoksów. Wobec tej różnorodności form spróbujmy dokonać klasyfikacji.
Paradoks – twierdzenie niezgodne z powszechnie przyjętym mniemaniem, rozumowanie, którego elementy są pozornie oczywiste, ale wskutek zawartego w nim błędu logicznego lub nieostrości wyrażeń prowadzące do wniosków sprzecznych ze sobą lub z uprzednio przyjętymi założeniami.
Encyklopedia Multimedialna PWN
Paradoks w sensie potocznym – twierdzenie niezgodne z powszechnie przyjętym mniemaniem. Matematyka zna wiele twierdzeń, nazywanych paradoksami dlatego, że choć uzyskane lege artis, stoją w sprzeczności z potoczną intuicją. To, na przykład, twierdzenie Banacha–Tarskiego orzekające o możliwości rozkładu kuli na skończenie wiele części, z których można złożyć dwie przystające do niej kule, lub paradoks Skolema–Löwenheima o istnieniu przeliczalnego modelu teorii mnogości, teorii, która swoją siłę zawdzięcza temu, że dopuszcza istnienie zbiorów nieprzeliczalnych.
Ten przypadek paradoksu nie jest dla nas interesujący, gdyż świadczy o intuicjach raczej niż o samej matematyce. Zajmiemy się natomiast innymi postaciami paradoksów, o których niżej.
Czytelnika zainteresowanego tematem ciągłości gorąco zachęcam do sięgnięcia po książkę pt. Ciągłość. Szkice z historii matematyki Jerzego Mioduszewskiego, WSiP 1996.
Aporia – trudność myślowa, wynikająca z nieumiejętności rozstrzygnięcia wartości argumentów za i przeciw pewnej tezie.
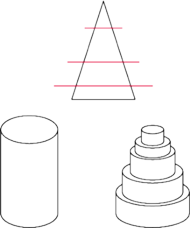
Najbardziej znane aporie pochodzą sprzed około 2500 lat, z okresu, gdy m.in. w środowisku eleatów rozwijały się początki rozumowania dedukcyjnego. Paradoksy Zenona z Elei, służące do uzasadnienia tezy o niezmienności i niepodzielności bytu, są powszechnie znane, przyjrzyjmy się więc podobnemu rozumowaniu Demokryta (przełom V i IV wieku p.n.e). Wyobraźmy sobie stożek, który przecinamy płaszczyznami równoległymi do podstawy. Czy pola przekrojów są jednakowe dla każdej płaszczyzny, czy różne dla różnych płaszczyzn? Jeśli jednakowe, to stożek jest w istocie walcem. Jeśli różne, to stożek musi być bryłą podobną do piętrowego tortu (rysunek). Nie ma zatem dobrej odpowiedzi.
Paradoks Demokryta jest bardzo bliski znanemu paradoksowi strzały Zenona z Elei. Chodzi tu o strukturę przestrzeni: jeśli odcinek (wysokość stożka) składa się z pojedynczych punktów, otrzymać musimy tort; jeśli jest nierozkładalną całością, otrzymujemy walec. Rozwiązanie przynosi dopiero nowożytne pojęcie przestrzeni, łączące oba te aspekty. Odcinek jest istotnie zbiorem punktów, jednak tzw. naturalny porządek tworzy z niego pewną całość, strukturę ciągłą bez luk i skoków, co tłumaczy ciągłą, a nie skokową zmianę pola przekroju stożka. Takie wyjaśnienie nie było jednak dostępne w czasach Demokryta i Zenona. Trudność wynikła z niedostatku dostępnego aparatu pojęciowego.
Przeskoczmy około 2400 lat, lądując na przełomie XIX i XX wieku. Teoria mnogości przekracza właśnie wiek niemowlęcy i wchodzi w dzieciństwo, legitymując się następującą definicją zbioru, wprowadzoną przez jej twórcę, niemieckiego matematyka Georga Cantora: „Zbiór to dowolna, traktowana jako całość mnogość M różnych dobrze określonych obiektów naszej intuicji lub umysłu, zwanych elementami M”.
Rozważmy zatem za Bertrandem Russellem, angielskim filozofem i logikiem,
zbiór
 określony następująco:
określony następująco:
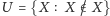 . Czy
. Czy
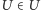 ? Proste rozumowanie wykazuje, że
? Proste rozumowanie wykazuje, że
 wtedy i tylko
wtedy, gdy
wtedy i tylko
wtedy, gdy
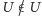 .
.
Paradoks Russella wynika z nader ogólnej definicji zbioru, dopuszczającej
tworzenie zbioru takiego jak
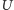 (który bez trudu ogarniamy umysłem jako
całość). Wśród różnych odpowiedzi na ten niepożądany w matematyce
paradoks przeważyła koncepcja oparcia teorii zbiorów na mocnych
fundamentach aksjomatycznych, stanowiących pośrednio precyzyjną definicję
zbioru, m.in. wykluczających możliwość tworzenia zbioru „wszystkich
elementów” spełniających dany warunek. Taki zbiór można zbudować tylko
z elementów zbioru już istniejącego. Źródłem paradoksu okazała się
nieostrość definicji.
(który bez trudu ogarniamy umysłem jako
całość). Wśród różnych odpowiedzi na ten niepożądany w matematyce
paradoks przeważyła koncepcja oparcia teorii zbiorów na mocnych
fundamentach aksjomatycznych, stanowiących pośrednio precyzyjną definicję
zbioru, m.in. wykluczających możliwość tworzenia zbioru „wszystkich
elementów” spełniających dany warunek. Taki zbiór można zbudować tylko
z elementów zbioru już istniejącego. Źródłem paradoksu okazała się
nieostrość definicji.
Antynomia – sprzeczność, wynikająca z rozumowania uznanego za poprawne i przesłanek uznanych za prawdziwe.
Poszukując antynomii, cofnijmy się ponownie do czasów greckich. Eubulidesowi
(IV wiek p.n.e.) przypisuje się wygłoszenie następującego zdania: „To, co teraz
mówię, jest kłamstwem.” To paradoks kłamcy, który w dzisiejszym języku
mogliśmy zapisać jako zdanie
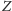 :
:
Zdanie
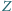 jest fałszywe.
jest fałszywe.
Zdanie
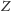 jest oczywiście prawdziwe wtedy i tylko wtedy, gdy jest
fałszywe.
jest oczywiście prawdziwe wtedy i tylko wtedy, gdy jest
fałszywe.
Rozumowanie z „paradoksu kłamcy” wydaje się sugerować, że problem bierze
się ze zbyt małej liczby wartości logicznych: zdanie niefałszywe uznajemy od
razu za prawdziwe. Pomyślmy zatem o logice, w której prawda i fałsz nie są
jedynymi wartościami logicznymi i zastanówmy się nad zdaniem
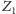 o treści następującej: Zdanie
o treści następującej: Zdanie
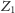 nie jest prawdziwe. Ponownie
otrzymujemy paradoksalną sprzeczność: zdanie
nie jest prawdziwe. Ponownie
otrzymujemy paradoksalną sprzeczność: zdanie
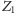 jest prawdziwe wtedy
i tylko wtedy, gdy nie jest prawdziwe.
jest prawdziwe wtedy
i tylko wtedy, gdy nie jest prawdziwe.
Mamy sytuację bardzo niepokojącą: poprawne rozumowanie prowadzi do paradoksalnego wniosku, mimo wprowadzenia nowych wartości logicznych.
Paradoks kłamcy bywa niekiedy przypisywany temu, że mamy do czynienia ze zdaniem, które orzeka samo o sobie. Obok widać jednak dwa zdania, z których żadne nie mówi samo o sobie, ale razem tworzą całość równie paradoksalną jak paradoks kłamcy. Czytelnik może sprawdzić, że można utworzyć zestaw trzech, czterech lub większej liczby zdań, które razem dadzą podobny efekt. Należałoby więc odrzucić możliwość powracania do pierwszego zdania, nawet jeśli po drodze przechodzimy przez kilka innych?
Popatrzmy na następny przykład. Dla każdego
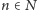 niech zdanie
niech zdanie
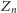 stwierdza co następuje: Dla każdego
stwierdza co następuje: Dla każdego
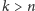 , zdanie
, zdanie
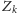 jest fałszywe. Jeśli zdanie
jest fałszywe. Jeśli zdanie
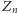 jest prawdziwe (dla pewnego
jest prawdziwe (dla pewnego
 ), to
wszystkie zdania
), to
wszystkie zdania
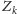 , gdy
, gdy
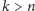 , są fałszywe, w szczególności
zdanie
, są fałszywe, w szczególności
zdanie
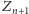 . Jednocześnie zdanie
. Jednocześnie zdanie
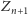 jest też prawdziwe, bo
wszystkie zdania
jest też prawdziwe, bo
wszystkie zdania
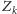 , gdy
, gdy
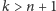 , są fałszywe – sprzeczność.
Wniosek: wszystkie zdania
, są fałszywe – sprzeczność.
Wniosek: wszystkie zdania
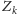 muszą być fałszywe. Ale wtedy
każde z nich jest prawdziwe i w rezultacie jednocześnie prawdziwe
i fałszywe!
muszą być fałszywe. Ale wtedy
każde z nich jest prawdziwe i w rezultacie jednocześnie prawdziwe
i fałszywe!
Budowanie zdań – jeśli nie ma prowadzić do paradoksów – musi zatem być
poddane pewnym rygorom, podobnie jak budowanie zbiorów. Przede
wszystkim, należy jasno rozróżniać poziomy języka. Jeśli zdanie
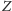 należy do jakiegoś języka (np. języka opisu pewnej rzeczywistości), to zdanie
mówiące o zdaniu
należy do jakiegoś języka (np. języka opisu pewnej rzeczywistości), to zdanie
mówiące o zdaniu
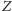 powinno być na poziomie wyższym niż poziom
samego zdania
powinno być na poziomie wyższym niż poziom
samego zdania
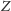 . Przy takim wymogu zdanie mówiące samo o sobie
zostałoby wykluczone jako niezgodne z regułami. Co więcej, hierarchia
poziomów nie może dopuszczać cykliczności, to znaczy jeśli poziom
. Przy takim wymogu zdanie mówiące samo o sobie
zostałoby wykluczone jako niezgodne z regułami. Co więcej, hierarchia
poziomów nie może dopuszczać cykliczności, to znaczy jeśli poziom
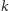 jest niższy niż poziom
jest niższy niż poziom
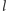 , to poziom
, to poziom
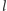 nie może być
niższy niż
nie może być
niższy niż
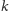 . W ten sposób eliminujemy cykle zdań, takie jak zdania
. W ten sposób eliminujemy cykle zdań, takie jak zdania
 i
i
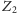 na marginesie. Wreszcie, hierarchia poziomów musi być
dobrze ugruntowana: schodząc na coraz niższy poziom, po skończonej liczbie
kroków musimy trafić na poziom, z którego już niżej nie ma dokąd
pójść. Pozbywamy się wtedy sytuacji takich, jak w nieskończonym ciągu
zdań powyżej.
na marginesie. Wreszcie, hierarchia poziomów musi być
dobrze ugruntowana: schodząc na coraz niższy poziom, po skończonej liczbie
kroków musimy trafić na poziom, z którego już niżej nie ma dokąd
pójść. Pozbywamy się wtedy sytuacji takich, jak w nieskończonym ciągu
zdań powyżej.
Jak widać, aporie i antynomie niekiedy skłaniały do istotnych zmian w konstrukcji teorii, niekiedy inspirowały ważne wyniki (dowód twierdzenia Gödla o niezupełności arytmetyki jest rozwiniętą trawestacją paradoksu kłamcy). Tak jak gorączka wskazuje na potrzebę interwencji lekarskiej, tak paradoksy wskazują na luki w konstrukcji teorii i na potrzebę interwencji jej twórców.
Pozostawiliśmy na boku jeszcze jeden rodzaj paradoksów: to te, które powstają w wyniku błędu logicznego. Ciekawe są zwłaszcza te zamierzone.
Sofizmat – rozumowanie często świadomie błędne, mające na celu oszukanie słuchacza lub czytelnika.
Przykład? Udowodnimy, że dla każdej liczby naturalnej
 prawdziwe
jest zdanie:
prawdziwe
jest zdanie:
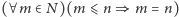 .
.
Dowód indukcyjny: Gdy
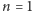 i
i
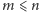 , to
, to
 ,
gdyż 1 jest najmniejszą liczbą naturalną. Załóżmy, że dla pewnej liczby
naturalnej
,
gdyż 1 jest najmniejszą liczbą naturalną. Załóżmy, że dla pewnej liczby
naturalnej
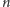 zdanie jest prawdziwe i niech
zdanie jest prawdziwe i niech
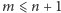 . Wtedy
. Wtedy
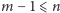 i z założenia indukcyjnego
i z założenia indukcyjnego
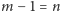 . Stąd już mamy
równość
. Stąd już mamy
równość
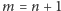 .
.
Czytelnik łatwo sam wywnioskuje z tego twierdzenia, iż
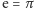 .
.
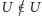 , to
, to
 spełnia warunek przynależności
do
spełnia warunek przynależności
do
 więc
więc
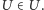 Jeśli
Jeśli
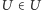 , to
, to
 nie spełnia
warunku przynależności do
nie spełnia
warunku przynależności do
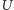 , a więc
, a więc
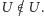
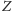 jest prawdziwe, to prawdą jest to, co orzeka, a więc
jest prawdziwe, to prawdą jest to, co orzeka, a więc
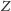 jest fałszywe. Jeśli natomiast
jest fałszywe. Jeśli natomiast
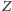 jest fałszywe, to nie jest prawdą
to, co głosi, a zatem nie jest fałszywe – jest więc prawdziwe.
jest fałszywe, to nie jest prawdą
to, co głosi, a zatem nie jest fałszywe – jest więc prawdziwe.
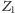 jest prawdziwe, to prawdą jest, że nie jest prawdziwe –
a więc nie jest prawdziwe. Jeśli natomiast zdanie
jest prawdziwe, to prawdą jest, że nie jest prawdziwe –
a więc nie jest prawdziwe. Jeśli natomiast zdanie
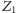 nie jest prawdziwe, to
orzeka prawdę, jest zatem prawdziwe.
nie jest prawdziwe, to
orzeka prawdę, jest zatem prawdziwe.
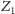 : Zdanie
: Zdanie
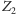 jest fałszywe.
jest fałszywe. 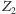 : Zdanie
: Zdanie
 jest
prawdziwe.
jest
prawdziwe.
 : Dla każdego
: Dla każdego
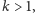
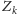 jest fałszywe.
jest fałszywe.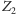 : Dla
każdego
: Dla
każdego
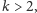
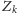 jest fałszywe.
jest fałszywe.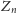 : Dla każdego
: Dla każdego
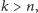
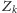 jest fałszywe.
jest fałszywe.