Klub 44M - zadania X 2019»Zadanie 788
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2019
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (383 KB)
-
Zadanie 788 zaproponował pan Zbigniew Skalik z Wrocławia (wskazując zadanie 716 z Delta 2/2016 jako źródło inspiracji).
Znaleźć największą liczbę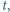 
dla której nierówność
 |
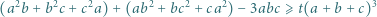zachodzi dla każdej trójki liczb dodatnich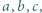 
będących długościami boków trójkąta.
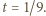Wykażemy, że wartość 
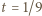gwarantuje spełnienie nierówności dla każdego trójkąta.
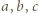dowolnego trójkąta można wyrazić przez trójkę liczb 
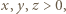pisząc: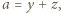 
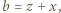
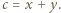Oznaczmy przez 
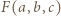różnicę między lewą oraz prawą stroną zadanej nierówności (z parametrem 
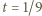); mamy uzasadnić, że 
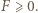Do dowodu użyjemy tożsamości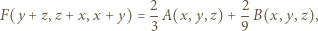
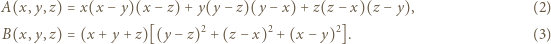
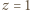oraz czterech różnych wartości 
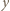(można też użyć programu komputerowego). Wyrażenia (2) i (3) mają dla 
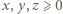wartości nieujemne: nierówność 
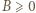jest oczywista; zaś 
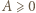to znana nierówność Schura. Stąd 
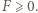Wniosek: szukana maksymalna wartość 
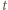wynosi 
.
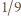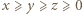; wówczas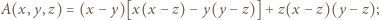
.
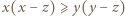