Klub 44M - zadania X 2019»Zadanie 787
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2019
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (383 KB)
Niech 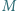 będzie dowolnym niepustym skończonym zbiorem liczb całkowitych. Dowieść, że można ustawić elementy zbioru
będzie dowolnym niepustym skończonym zbiorem liczb całkowitych. Dowieść, że można ustawić elementy zbioru 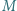 w ciąg
w ciąg 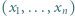 tak, by dla każdej trójki wskaźników
tak, by dla każdej trójki wskaźników 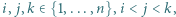 spełniony był warunek:
spełniony był warunek: 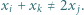

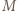 o dowolną liczbę całkowitą. Można więc zakładać, że jego elementami są liczby nieujemne. Zauważmy też, że jeśli elementy pewnego zbioru
o dowolną liczbę całkowitą. Można więc zakładać, że jego elementami są liczby nieujemne. Zauważmy też, że jeśli elementy pewnego zbioru 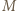 da się uporządkować w wymagany sposób, wówczas to samo uporządkowanie jest dobre dla każdego podzbioru zbioru
da się uporządkować w wymagany sposób, wówczas to samo uporządkowanie jest dobre dla każdego podzbioru zbioru 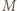 (po wykreśleniu zbędnych elementów).
(po wykreśleniu zbędnych elementów).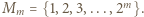 Dla
Dla 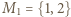 każde z dwóch uporządkowań jest dobre (warunek spełniony "w próżni"). Dalej indukcja: przyjmijmy, że dla pewnego
każde z dwóch uporządkowań jest dobre (warunek spełniony "w próżni"). Dalej indukcja: przyjmijmy, że dla pewnego 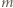 zbiór
zbiór 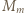 daje się ustawić w ciąg
daje się ustawić w ciąg 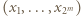 tak, że
tak, że 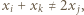 gdy
gdy 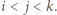 Wówczas ciąg
Wówczas ciąg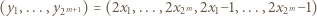
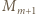 (jednym z możliwych); bo gdy
(jednym z możliwych); bo gdy 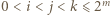 lub
lub 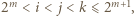 nierówność
nierówność 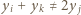 wynika z założenia indukcyjnego; gdy zaś
wynika z założenia indukcyjnego; gdy zaś 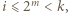 liczba
liczba 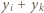 jest nieparzysta, więc
jest nieparzysta, więc 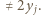 To kończy krok indukcyjny.
To kończy krok indukcyjny.