Zadanie ZM-1615
o zadaniu...
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
Udowodnić, że dla dowolnych liczb naturalnych 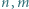 liczba rozwiązań nierówności
liczba rozwiązań nierówności 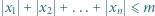 w liczbach całkowitych jest równa liczbie rozwiązań nierówności
w liczbach całkowitych jest równa liczbie rozwiązań nierówności 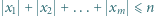 w liczbach całkowitych.
w liczbach całkowitych.

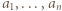 spełniają
spełniają 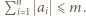 Możemy na dwa sposoby wskazać
Możemy na dwa sposoby wskazać 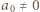 takie, że
takie, że 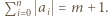 Każdy ciąg
Każdy ciąg 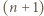 liczb spełniający tę równość (oraz
liczb spełniający tę równość (oraz 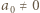 ) możemy podzielić na bloki, czyli fragmenty postaci
) możemy podzielić na bloki, czyli fragmenty postaci 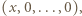 gdzie
gdzie 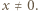 Jeśli długość takiego bloku to
Jeśli długość takiego bloku to 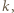 to przyporządkujemy mu blok
to przyporządkujemy mu blok 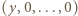 długości
długości 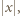 gdzie
gdzie 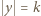 oraz
oraz 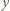 jest tego samego znaku, co
jest tego samego znaku, co 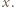 Wykonując tę operację na wszystkich blokach, dostaniemy ciąg
Wykonując tę operację na wszystkich blokach, dostaniemy ciąg 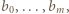 gdzie
gdzie 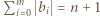 i
i 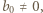 co daje nam ciąg liczb całkowitych
co daje nam ciąg liczb całkowitych 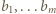 spełniający
spełniający 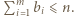 Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.
Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.