- Narzędzia
- Obiekty
- Strategie
- Słowa kluczowe
- Kategoria
- Matematyka
Zadanie ZM-K44-559
o zadaniu...
- Publikacja w Delcie: sierpień 2008
- Publikacja elektroniczna: 2 lutego 2011
Na wolnych polach kwadratowej planszy o rozmiarach
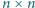 dwaj gracze
na przemian stawiają pionki (nierozróżnialne). Wygrywa gracz, po którego
ruchu znajdą się cztery pionki na dowolnych czterech polach, będących
narożnikami prostokąta o bokach równoległych do krawędzi planszy.
Rozstrzygnąć (w zależności od
dwaj gracze
na przemian stawiają pionki (nierozróżnialne). Wygrywa gracz, po którego
ruchu znajdą się cztery pionki na dowolnych czterech polach, będących
narożnikami prostokąta o bokach równoległych do krawędzi planszy.
Rozstrzygnąć (w zależności od
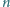 ), który z graczy ma strategię
zwycięską – rozpoczynający czy jego przeciwnik.
), który z graczy ma strategię
zwycięską – rozpoczynający czy jego przeciwnik.
Rozwiązanie
Gdy
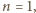 nikt nie może wygrać. Dalej zakładamy, że
nikt nie może wygrać. Dalej zakładamy, że
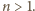 Rząd pionowy (kolumnę) lub poziomy (wiersz), którego wszystkie pola są wolne,
nazwiemy pustym. Przypuśćmy, że w pewnym momencie niezakończonej
gry sytuacja na planszy spełnia następujące warunki:
Rząd pionowy (kolumnę) lub poziomy (wiersz), którego wszystkie pola są wolne,
nazwiemy pustym. Przypuśćmy, że w pewnym momencie niezakończonej
gry sytuacja na planszy spełnia następujące warunki:
- (a)
- liczba pustych wierszy jest parzysta oraz liczba pustych kolumn jest parzysta;
- (b)
- jeśli w pewnym wierszu [kolumnie] co najmniej dwa pola są zajęte, to są one jedynymi zajętymi polami w swoich kolumnach [wierszach].
Taką sytuację będziemy nazywać strategiczną.
Z warunku (b) wynika, że gracz
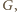 do którego należy ruch,
nie jest w stanie w tym ruchu wygrać. Zajmuje jakieś pole
do którego należy ruch,
nie jest w stanie w tym ruchu wygrać. Zajmuje jakieś pole
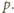 Wskażemy taktykę dla gracza
Wskażemy taktykę dla gracza
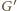 (jego przeciwnika), rozważając trzy
przypadki.
(jego przeciwnika), rozważając trzy
przypadki.
- 1.
- Jeżeli pole
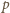 leży na przecięciu wiersza i kolumny, które do
tego momentu były puste, to
leży na przecięciu wiersza i kolumny, które do
tego momentu były puste, to
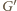 zajmuje pole leżące na przecięciu
innego wiersza i innej kolumny, które nadal są puste (a istnieją,
w myśl warunku (a)). Liczba pustych wierszy oraz liczba pustych
kolumn zmniejszają się o 2. Nowa sytuacja jest znów strategiczna.
zajmuje pole leżące na przecięciu
innego wiersza i innej kolumny, które nadal są puste (a istnieją,
w myśl warunku (a)). Liczba pustych wierszy oraz liczba pustych
kolumn zmniejszają się o 2. Nowa sytuacja jest znów strategiczna.
- 2.
- Jeżeli pole
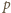 leży na przecięciu wiersza i kolumny, które przed
ruchem gracza
leży na przecięciu wiersza i kolumny, które przed
ruchem gracza
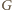 były niepuste, to jest ono – po ruchu
były niepuste, to jest ono – po ruchu
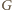 – jednym z trzech zajętych narożników pewnego prostokąta; pole
w czwartym narożniku jest wolne (co wynika z warunku (b)); zajmując
teraz to pole, gracz
– jednym z trzech zajętych narożników pewnego prostokąta; pole
w czwartym narożniku jest wolne (co wynika z warunku (b)); zajmując
teraz to pole, gracz
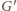 wygrywa.
wygrywa.
- 3.
- Jeżeli pole
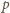 leży na przecięciu pustej (do tej pory) kolumny
leży na przecięciu pustej (do tej pory) kolumny
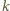 i niepustego wiersza
i niepustego wiersza
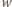 (lub odwrotnie; przyjmijmy, że właśnie tak),
to rozważamy podprzypadki:
(lub odwrotnie; przyjmijmy, że właśnie tak),
to rozważamy podprzypadki:
- 3.1
- Gdy istnieje kolumna różna od
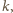 w której zajęte są
dwa pola – w tym jedno w wierszu
w której zajęte są
dwa pola – w tym jedno w wierszu
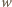 – to (podobnie
jak w przypadku
– to (podobnie
jak w przypadku
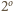 ) te dwa pola wraz z polem
) te dwa pola wraz z polem
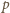 są
trzema narożnikami prostokąta, w którego czwartym narożniku
jest wolne pole (warunek (b)); zajmując to pole, gracz
są
trzema narożnikami prostokąta, w którego czwartym narożniku
jest wolne pole (warunek (b)); zajmując to pole, gracz
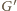 wygrywa.
wygrywa.
- 3.2
- Gdy wszystkie zajęte pola wiersza
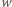 są jedynymi
zajętymi polami w swoich kolumnach, wówczas korzystamy znów
z warunku (a), zapewniającego, że przed ruchem
są jedynymi
zajętymi polami w swoich kolumnach, wówczas korzystamy znów
z warunku (a), zapewniającego, że przed ruchem
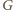 istniała
jeszcze co najmniej jedna pusta kolumna. Gracz
istniała
jeszcze co najmniej jedna pusta kolumna. Gracz
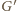 zajmuje
pole w tej kolumnie, w wierszu
zajmuje
pole w tej kolumnie, w wierszu
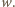 Liczba pustych wierszy
nie zmienia się, liczba pustych kolumn zmniejsza się o 2. Powstała
sytuacja i tym razem jest strategiczna.
Liczba pustych wierszy
nie zmienia się, liczba pustych kolumn zmniejsza się o 2. Powstała
sytuacja i tym razem jest strategiczna.
Gracz
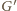 może więc uniknąć porażki, stale lokując gracza
może więc uniknąć porażki, stale lokując gracza
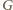 w sytuacji strategicznej, dopóki nie zdarzy się przypadek 2 lub 3.1 – co musi
nastąpić, bowiem gra jest skończona i prostokąt na planszy pojawić się
musi.
w sytuacji strategicznej, dopóki nie zdarzy się przypadek 2 lub 3.1 – co musi
nastąpić, bowiem gra jest skończona i prostokąt na planszy pojawić się
musi.
Gdy
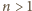 jest liczbą nieparzystą, gracz rozpoczynający zajmuje na starcie
dowolne pole i tworzy sytuację strategiczną, stawiając przeciwnika w roli
gracza
jest liczbą nieparzystą, gracz rozpoczynający zajmuje na starcie
dowolne pole i tworzy sytuację strategiczną, stawiając przeciwnika w roli
gracza
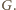 Stosując następnie opisane postępowanie, rozpoczynający
zapewnia sobie zwycięstwo. Gdy zaś
Stosując następnie opisane postępowanie, rozpoczynający
zapewnia sobie zwycięstwo. Gdy zaś
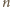 jest liczbą parzystą, to już
sytuacja wyjściowa (pusta plansza) jest strategiczna i role się odwracają –
rozpoczynający przegrywa.
jest liczbą parzystą, to już
sytuacja wyjściowa (pusta plansza) jest strategiczna i role się odwracają –
rozpoczynający przegrywa.
