Zadanie ZM-1524
o zadaniu...
- Publikacja w Delcie: marzec 2017
- Publikacja elektroniczna: 1 marca 2017
Udowodnić, że dla każdego 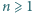 istnieje ciąg arytmetyczny
istnieje ciąg arytmetyczny  dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
Wskazówka. W rozwiązaniu można skorzystać z twierdzenia o liczbach pierwszych, na przykład używając szacowania 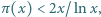 prawdziwego dla dostatecznie dużych
prawdziwego dla dostatecznie dużych 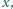 gdzie
gdzie 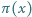 oznacza liczbę liczb pierwszych nie większych od
oznacza liczbę liczb pierwszych nie większych od 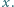

 będzie dodatnią liczbą całkowitą. Zauważmy, że każda mniejsza od
będzie dodatnią liczbą całkowitą. Zauważmy, że każda mniejsza od 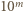 wielokrotność liczby
wielokrotność liczby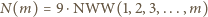
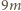 i podzielna przez
i podzielna przez 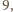 więc jest dzielnikiem liczby
więc jest dzielnikiem liczby 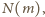 a tym bardziej dowolnej jej wielokrotności.
a tym bardziej dowolnej jej wielokrotności.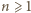 można dobrać takie
można dobrać takie 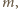 aby spełniona była nierówność
aby spełniona była nierówność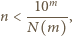
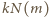 dla
dla 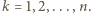
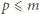 wchodzi do rozkładu liczby
wchodzi do rozkładu liczby 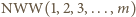 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem 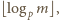 a zatem nie większym od
a zatem nie większym od 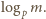 Wobec tego
Wobec tego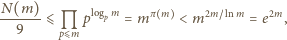
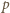 oraz skorzystaliśmy z nierówności zasugerowanej we wskazówce do zadania (prawdziwej dla
oraz skorzystaliśmy z nierówności zasugerowanej we wskazówce do zadania (prawdziwej dla 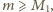 gdzie
gdzie 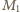 jest pewną dodatnią liczbą całkowitą).
jest pewną dodatnią liczbą całkowitą).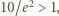 więc
więc 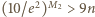 dla pewnej dodatniej liczby całkowitej
dla pewnej dodatniej liczby całkowitej 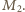 Do zakończenia rozwiązania wystarczy przyjąć
Do zakończenia rozwiązania wystarczy przyjąć 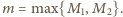
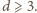 Nie rozstrzyga ono jednak, czy istnieją dowolne długie ciągi arytmetyczne liczb naturalnych, które są podzielne przez sumę swoich cyfr w zapisie dwójkowym.
Nie rozstrzyga ono jednak, czy istnieją dowolne długie ciągi arytmetyczne liczb naturalnych, które są podzielne przez sumę swoich cyfr w zapisie dwójkowym.