Zadanie ZM-1493
o zadaniu...
- Publikacja w Delcie: maj 2016
- Publikacja elektroniczna: 1 maja 2016
W wierzchołkach dwunastościanu foremnego umieszczamy parami różne liczby naturalne, a następnie każdej krawędzi przypisujemy największy wspólny dzielnik liczb z jej końców. Czy możemy zrobić to w taki sposób, by suma liczb w wierzchołkach była równa sumie liczb na krawędziach?
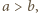to mamy 
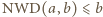oraz 
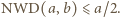W takim razie 
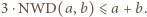Ponieważ suma liczb na krawędziach jest równa sumie liczb w wierzchołkach, mamy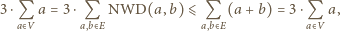
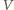i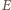 
odpowiadają zbiorom wierzchołków i krawędzi dwunastościanu. Dla każdej krawędzi o końcach 
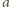i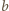 
zachodzi więc równość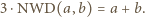
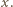W każdym z trzech sąsiadujących z nim wierzchołków jest liczba 
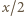lub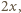 
co jest sprzeczne z założeniem o przyporządkowaniu wierzchołkom parami różnych liczb.