Załóżmy więc, że liczby całkowite 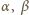 i
i 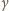 są niepodzielne przez liczbę pierwszą
są niepodzielne przez liczbę pierwszą 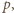 oraz że dla pewnej trójki liczb całkowitych nieujemnych
oraz że dla pewnej trójki liczb całkowitych nieujemnych 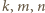 zachodzą równości
zachodzą równości 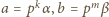 i
i 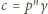 (w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn
(w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn 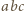 jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez
jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez 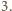 Mamy
Mamy 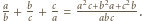 Mianownik tego ułamka jest podzielny przez liczbę
Mianownik tego ułamka jest podzielny przez liczbę 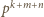 i niepodzielny przez
i niepodzielny przez 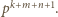 Zastąpienie uporządkowanej trójki liczb
Zastąpienie uporządkowanej trójki liczb 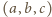 trójką
trójką 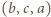 lub
lub 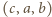 powoduje, że liczba
powoduje, że liczba 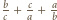 lub
lub 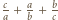 - więc ta z treści zadania - ma być całkowita (trójka
- więc ta z treści zadania - ma być całkowita (trójka 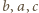 to jednak coś innego, bo na ogół
to jednak coś innego, bo na ogół 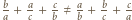 ). Można więc założyć, że
). Można więc założyć, że 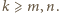 Mamy
Mamy
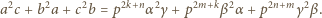
- Jeśli
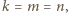 to
to 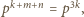 więc
więc 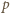 występuje w rozkładzie iloczynu
występuje w rozkładzie iloczynu 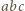 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem 
- Jeśli
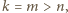 to
to 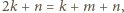
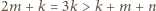 i
i 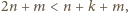 więc dwa z trzech składników licznika dzielą się przez
więc dwa z trzech składników licznika dzielą się przez 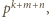 a trzeci nie, co oznacza, że liczba
a trzeci nie, co oznacza, że liczba 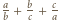 nie jest całkowita, wbrew założeniu.
nie jest całkowita, wbrew założeniu.
- Jeśli
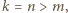 to
to 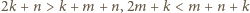 i
i 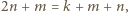 więc znów liczba
więc znów liczba 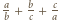 nie jest całkowita.
nie jest całkowita.
- Jeśli
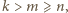 to
to 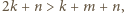
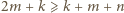 i
i 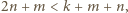 więc znów liczba
więc znów liczba 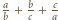 nie jest całkowita.
nie jest całkowita.
- Jeśli
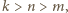 to
to 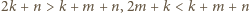 i
i 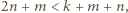 to teraz dwa składniki nie dzielą się przez
to teraz dwa składniki nie dzielą się przez 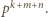 Ich suma może dzielić się przez
Ich suma może dzielić się przez 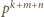 tylko wtedy, gdy
tylko wtedy, gdy 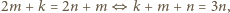 więc w tym wypadku liczba
więc w tym wypadku liczba 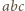 jest podzielna przez
jest podzielna przez 
Wykazaliśmy, że jeśli liczba 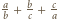 jest całkowita, to liczba pierwsza
jest całkowita, to liczba pierwsza 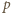 wchodzi w rozkład liczby
wchodzi w rozkład liczby 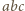 na czynniki pierwsze z wykładnikiem podzielnym przez
na czynniki pierwsze z wykładnikiem podzielnym przez 
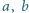 i
i  różne od zera, że liczba
różne od zera, że liczba 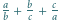 jest całkowita. Wykazać, że iloczyn
jest całkowita. Wykazać, że iloczyn 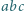 jest sześcianem liczby całkowitej.
jest sześcianem liczby całkowitej.
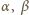 i
i 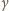 są niepodzielne przez liczbę pierwszą
są niepodzielne przez liczbę pierwszą 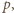 oraz że dla pewnej trójki liczb całkowitych nieujemnych
oraz że dla pewnej trójki liczb całkowitych nieujemnych 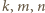 zachodzą równości
zachodzą równości 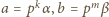 i
i 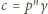 (w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn
(w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn 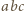 jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez
jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez 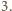 Mamy
Mamy 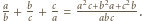 Mianownik tego ułamka jest podzielny przez liczbę
Mianownik tego ułamka jest podzielny przez liczbę 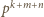 i niepodzielny przez
i niepodzielny przez 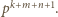 Zastąpienie uporządkowanej trójki liczb
Zastąpienie uporządkowanej trójki liczb 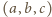 trójką
trójką 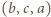 lub
lub 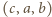 powoduje, że liczba
powoduje, że liczba 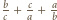 lub
lub 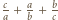 - więc ta z treści zadania - ma być całkowita (trójka
- więc ta z treści zadania - ma być całkowita (trójka 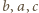 to jednak coś innego, bo na ogół
to jednak coś innego, bo na ogół 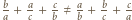 ). Można więc założyć, że
). Można więc założyć, że 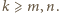 Mamy
Mamy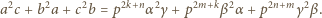
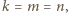 to
to 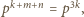 więc
więc 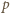 występuje w rozkładzie iloczynu
występuje w rozkładzie iloczynu 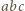 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem 
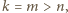 to
to 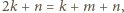
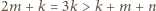 i
i 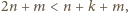 więc dwa z trzech składników licznika dzielą się przez
więc dwa z trzech składników licznika dzielą się przez 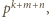 a trzeci nie, co oznacza, że liczba
a trzeci nie, co oznacza, że liczba 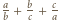 nie jest całkowita, wbrew założeniu.
nie jest całkowita, wbrew założeniu.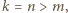 to
to 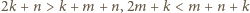 i
i 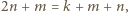 więc znów liczba
więc znów liczba 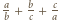 nie jest całkowita.
nie jest całkowita.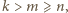 to
to 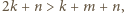
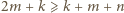 i
i 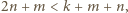 więc znów liczba
więc znów liczba 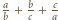 nie jest całkowita.
nie jest całkowita.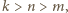 to
to 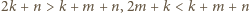 i
i 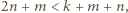 to teraz dwa składniki nie dzielą się przez
to teraz dwa składniki nie dzielą się przez 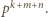 Ich suma może dzielić się przez
Ich suma może dzielić się przez 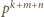 tylko wtedy, gdy
tylko wtedy, gdy 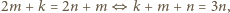 więc w tym wypadku liczba
więc w tym wypadku liczba 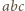 jest podzielna przez
jest podzielna przez 
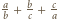 jest całkowita, to liczba pierwsza
jest całkowita, to liczba pierwsza 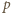 wchodzi w rozkład liczby
wchodzi w rozkład liczby 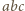 na czynniki pierwsze z wykładnikiem podzielnym przez
na czynniki pierwsze z wykładnikiem podzielnym przez 