Matematyka jest jedna: metoda probabilistyczna»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Matematyka jest jedna: metoda probabilistyczna
- Publikacja w Delcie: kwiecień 2015
- Publikacja elektroniczna: 31-03-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (101 KB)
Dana jest liczba całkowita dodatnia 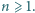 Niech
Niech 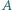 będzie ustalonym zbiorem
będzie ustalonym zbiorem 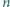 reszt z dzielenia przez
reszt z dzielenia przez 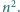 Udowodnić, że istnieje zbiór
Udowodnić, że istnieje zbiór 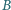 złożony z
złożony z 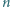 reszt z dzielenia przez
reszt z dzielenia przez 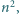 który spełnia następujący warunek: co najmniej połowa reszt z dzielenia przez
który spełnia następujący warunek: co najmniej połowa reszt z dzielenia przez 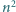 przystaje do liczby postaci
przystaje do liczby postaci 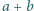 dla
dla 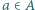 oraz
oraz 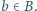

 niezależnych losowań ze zbioru reszt z dzielenia przez
niezależnych losowań ze zbioru reszt z dzielenia przez 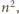 zakładając przy tym, że prawdopodobieństwo wylosowania dowolnej z reszt jest równe
zakładając przy tym, że prawdopodobieństwo wylosowania dowolnej z reszt jest równe 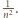 Z uzyskanych reszt tworzymy zbiór
Z uzyskanych reszt tworzymy zbiór 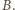 Ponieważ losowania są niezależne, może on składać się z mniej niż
Ponieważ losowania są niezależne, może on składać się z mniej niż 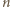 reszt, gdyż pewna reszta mogła zostać wylosowana więcej niż jeden raz. Jeżeli spełniony jest jednak warunek, w którym co najmniej połowa reszt może być zapisana w postaci
reszt, gdyż pewna reszta mogła zostać wylosowana więcej niż jeden raz. Jeżeli spełniony jest jednak warunek, w którym co najmniej połowa reszt może być zapisana w postaci 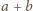 dla
dla 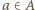 oraz
oraz 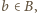 to możemy dopełnić zbiór
to możemy dopełnić zbiór 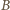 do zbioru
do zbioru 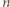 -elementowego w dowolny sposób i warunek ten pozostanie spełniony.
-elementowego w dowolny sposób i warunek ten pozostanie spełniony.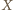 będzie liczbą reszt, które przystają do liczby postaci
będzie liczbą reszt, które przystają do liczby postaci 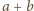 dla
dla 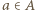 oraz
oraz 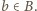 Wystarczy udowodnić, że wartość oczekiwana zmiennej losowej
Wystarczy udowodnić, że wartość oczekiwana zmiennej losowej 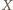 wynosi co najmniej
wynosi co najmniej 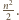 Ustalmy dowolną resztę
Ustalmy dowolną resztę 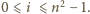 Ponieważ zbiór
Ponieważ zbiór 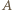 składa się z
składa się z  elementów, więc istnieje dokładnie
elementów, więc istnieje dokładnie  takich reszt
takich reszt 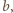 że
że 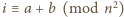 dla pewnego
dla pewnego 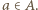 Prawdopodobieństwo tego, że ustalona reszta
Prawdopodobieństwo tego, że ustalona reszta 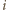 nie może być zapisana w żądanej postaci, wynosi zatem
nie może być zapisana w żądanej postaci, wynosi zatem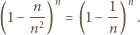
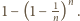 Korzystając z definicji wartości oczekiwanej oraz nierówności
Korzystając z definicji wartości oczekiwanej oraz nierówności 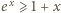 dla
dla 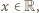 dostajemy
dostajemy![n2 ]=n2(1−(1−1))⩾n2(1−e−1)>n2(1−1)=n. E[X n22](/math/temat/matematyka/teoria_liczb/zadania/2015/03/29/zm-15_04-metody-4/19x-a985e63156cd220a3019db9f29340e69c1657a0c-dm-66,57,43-FF,FF,FF.gif)