Przypuśćmy przeciwnie, że po pewnej liczbie kroków zmazaliśmy
wszystkie liczby. Powiedzmy, że w ostatnim kroku wybraliśmy liczbę
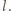 Skoro została ona zmazana, to
Skoro została ona zmazana, to
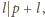 czyli również
czyli również
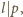 a zatem
a zatem
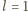 lub
lub
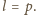
Wykażemy najpierw, że musieliśmy wykonać co najmniej trzy kroki. Jest
jasne, że wykonaliśmy więcej niż jeden. Przypuśćmy więc, że po
dwóch krokach wszystkie liczby zostały zmazane. Niech
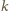 i
i
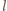 będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
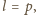 co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
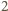 i
i
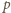 lub tylko
lub tylko
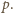 Ponieważ
Ponieważ
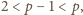 więc
więc
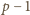 zmazaliśmy w pierwszym kroku, a zatem
zmazaliśmy w pierwszym kroku, a zatem
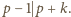 Natomiast z nierówności
Natomiast z nierówności
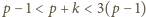 wynika, że
wynika, że
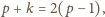 czyli
czyli
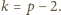 Ale
Ale
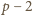 też musiało
zostać zmazane w pierwszym kroku, więc
też musiało
zostać zmazane w pierwszym kroku, więc
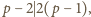 co jest
niemożliwe.
co jest
niemożliwe.
Załóżmy teraz, że w przedostatnim kroku (który nie jest jednocześnie
pierwszym) wybraliśmy liczbę
 Ta liczba nie została zmazana w tym
kroku, gdyż
Ta liczba nie została zmazana w tym
kroku, gdyż
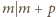 oznacza, że
oznacza, że
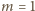 lub
lub
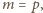 ale 1
zniknęła w pierwszym kroku, a
ale 1
zniknęła w pierwszym kroku, a
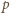 musi być wybrane w ostatnim. Zatem
musi być wybrane w ostatnim. Zatem
 zmazujemy w ostatnim kroku, czyli
zmazujemy w ostatnim kroku, czyli
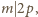 więc
więc
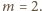 Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
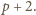 Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.
Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.
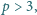 taka, że
taka, że
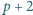 też jest pierwsza.
Na tablicy napisano liczby
też jest pierwsza.
Na tablicy napisano liczby
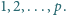 W każdym kroku wybieramy
jedną z nich, powiedzmy
W każdym kroku wybieramy
jedną z nich, powiedzmy
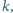 po czym zmazujemy wszystkie dzielniki
liczby
po czym zmazujemy wszystkie dzielniki
liczby
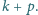 Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.

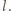 Skoro została ona zmazana, to
Skoro została ona zmazana, to
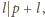 czyli również
czyli również
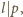 a zatem
a zatem
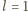 lub
lub
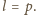
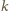 i
i
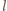 będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
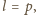 co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
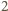 i
i
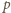 lub tylko
lub tylko
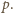 Ponieważ
Ponieważ
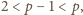 więc
więc
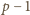 zmazaliśmy w pierwszym kroku, a zatem
zmazaliśmy w pierwszym kroku, a zatem
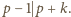 Natomiast z nierówności
Natomiast z nierówności
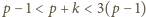 wynika, że
wynika, że
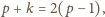 czyli
czyli
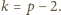 Ale
Ale
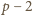 też musiało
zostać zmazane w pierwszym kroku, więc
też musiało
zostać zmazane w pierwszym kroku, więc
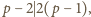 co jest
niemożliwe.
co jest
niemożliwe.
 Ta liczba nie została zmazana w tym
kroku, gdyż
Ta liczba nie została zmazana w tym
kroku, gdyż
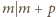 oznacza, że
oznacza, że
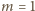 lub
lub
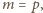 ale 1
zniknęła w pierwszym kroku, a
ale 1
zniknęła w pierwszym kroku, a
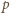 musi być wybrane w ostatnim. Zatem
musi być wybrane w ostatnim. Zatem
 zmazujemy w ostatnim kroku, czyli
zmazujemy w ostatnim kroku, czyli
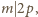 więc
więc
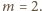 Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
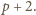 Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.
Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.