Zadanie ZM-1380
o zadaniu...
- Publikacja w Delcie: marzec 2013
- Publikacja elektroniczna: 01-03-2013
Dana jest liczba nieparzysta
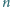 i liczby całkowite dodatnie względnie
pierwsze
i liczby całkowite dodatnie względnie
pierwsze
 i
i
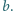 Udowodnić, że liczba
Udowodnić, że liczba
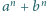 jest
podzielna przez
jest
podzielna przez
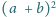 wtedy i tylko wtedy, gdy liczba
wtedy i tylko wtedy, gdy liczba
 jest
podzielna przez
jest
podzielna przez
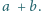

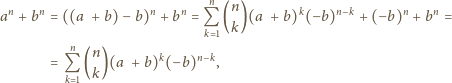
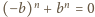 dla nieparzystych
dla nieparzystych
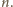 Zatem
Zatem
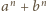 przy dzieleniu przez
przy dzieleniu przez
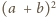 daje taką samą resztę jak
składnik odpowiadający
daje taką samą resztę jak
składnik odpowiadający
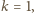 który wynosi
który wynosi
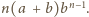 Zatem
Zatem
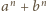 jest podzielne przez
jest podzielne przez
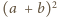 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
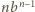 jest podzielne przez
jest podzielne przez
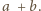 Ponieważ
Ponieważ
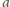 i
i
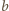 są
względnie pierwsze, względnie pierwsze są również
są
względnie pierwsze, względnie pierwsze są również
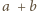 i
i
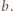 Stąd
otrzymujemy tezę.
Stąd
otrzymujemy tezę.