Zadanie ZM-1345
o zadaniu...
- Publikacja w Delcie: kwiecień 2012
- Publikacja elektroniczna: 01-04-2012
Dany jest wielomian
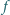 o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
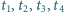 , że
, że

Udowodnić, że nie istnieje liczba całkowita
 , dla której
, dla której
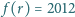 .
.

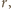 dla
której
dla
której
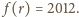 Korzystając z tego, że
Korzystając z tego, że
 dzieli
dzieli
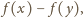 dla dowolnych liczb całkowitych
dla dowolnych liczb całkowitych
 i
i
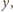 mamy
mamy

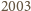 jest pierwsza, więc skoro liczby
jest pierwsza, więc skoro liczby
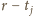 są parami różne,
to bez straty ogólności możemy przyjąć, że
są parami różne,
to bez straty ogólności możemy przyjąć, że

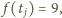 więc po podzieleniu z resztą wielomianu
więc po podzieleniu z resztą wielomianu
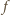 przez wielomian
przez wielomian
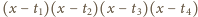 mamy
mamy
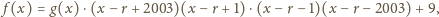
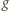 o współczynnikach całkowitych.
Podstawiając
o współczynnikach całkowitych.
Podstawiając
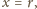 dostajemy
dostajemy
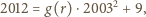
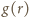 jest liczbą całkowitą.
jest liczbą całkowitą.