Klub 44M - zadania XI 2011»Zadanie 629
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2011
- Publikacja w Delcie: listopad 2011
- Publikacja elektroniczna: 1 listopada 2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (62 KB)
Niech
 będzie liczbą naturalną większą od 2. Dowieść, że ze zbioru
będzie liczbą naturalną większą od 2. Dowieść, że ze zbioru
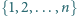 można usunąć dwie liczby tak, by suma liczb, które
pozostały, była kwadratem liczby naturalnej.
można usunąć dwie liczby tak, by suma liczb, które
pozostały, była kwadratem liczby naturalnej.

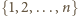 wynosi
wynosi
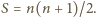 Suma dwóch liczb z tego zbioru może być
dowolną liczbą naturalną od 3 do
Suma dwóch liczb z tego zbioru może być
dowolną liczbą naturalną od 3 do
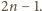 Usuwamy dwie –
suma liczb, które pozostały, może być dowolną liczbą naturalną od
Usuwamy dwie –
suma liczb, które pozostały, może być dowolną liczbą naturalną od
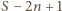 do
do
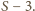 Wystarczy wykazać, że w przedziale
Wystarczy wykazać, że w przedziale
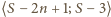 znajduje się jakiś kwadrat liczby naturalnej.
znajduje się jakiś kwadrat liczby naturalnej.
 będzie największą liczbą naturalną, której kwadrat
nie przekracza
będzie największą liczbą naturalną, której kwadrat
nie przekracza
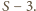 Wówczas
Wówczas
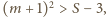 skąd
skąd
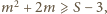 czyli
czyli
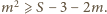 Wystarczy wykazać, że
prawa strona ostatniej nierówności jest nie mniejsza niż
Wystarczy wykazać, że
prawa strona ostatniej nierówności jest nie mniejsza niż
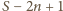 ; czyli
że zachodzi nierówność
; czyli
że zachodzi nierówność
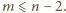 Dla
Dla
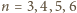 różnica
różnica
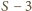 wynosi kolejno
wynosi kolejno
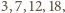 co daje wartości
co daje wartości
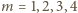 ;
mamy równość
;
mamy równość
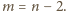 Dla
Dla
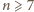 szacujemy kwadrat liczby
szacujemy kwadrat liczby
 :
:
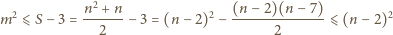
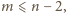 którą chcieliśmy wykazać.
którą chcieliśmy wykazać.