Zadanie ZM-1324
o zadaniu...
- Publikacja w Delcie: wrzesień 2011
- Publikacja elektroniczna: 31-08-2011
Niech
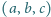 będzie trójką liczb całkowitych dodatnich spełniających
równanie
będzie trójką liczb całkowitych dodatnich spełniających
równanie
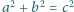 . Udowodnić, że nie istnieje liczba naturalna
. Udowodnić, że nie istnieje liczba naturalna
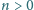 , dla której liczba
, dla której liczba
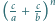 byłaby całkowita.
byłaby całkowita.

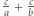 jest całkowita wtedy i tylko wtedy, gdy liczba
jest całkowita wtedy i tylko wtedy, gdy liczba
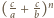 jest całkowita. Wystarczy zatem rozważyć przypadek
jest całkowita. Wystarczy zatem rozważyć przypadek
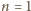 . Załóżmy nie wprost, że
. Załóżmy nie wprost, że
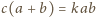 dla pewnej
liczby całkowitej
dla pewnej
liczby całkowitej
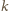 . Wiemy, że
. Wiemy, że
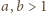 . Możemy założyć
bez utraty ogólności, że
. Możemy założyć
bez utraty ogólności, że
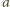 i
i
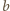 są względnie pierwsze
(jeśli nie są, to ich wspólny dzielnik dzieli też
są względnie pierwsze
(jeśli nie są, to ich wspólny dzielnik dzieli też
 i możemy
podzielić przez niego wszystkie trzy dane liczby). Wówczas
i możemy
podzielić przez niego wszystkie trzy dane liczby). Wówczas
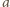 i
i
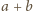 też są względnie pierwsze. Zatem, skoro
też są względnie pierwsze. Zatem, skoro
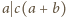 ,
to
,
to
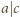 . Ale wtedy
. Ale wtedy
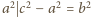 , więc
, więc
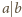 , co daje
sprzeczność.
, co daje
sprzeczność.