VI Olimpiada Matematyczna Gimnazjalistów»Zadanie 7
o zadaniu...
- Zadanie olimpijskie: VI Olimpiada Matematyczna Gimnazjalistów
- Zadanie pochodzi z artykułu VI Olimpiada Matematyczna Gimnazjalistów
- Publikacja w Delcie: styczeń 2011
- Publikacja elektroniczna: 20-12-2010
Udowodnij, że nie istnieją liczby nieparzyste
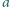 i
i
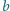 spełniające
równanie
spełniające
równanie
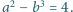

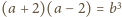 . Liczby
. Liczby
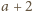 i
i
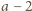 są nieparzyste i różnią się o
są nieparzyste i różnią się o
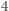 . Jeżeli
. Jeżeli
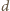 jest wspólnym dzielnikiem liczb
jest wspólnym dzielnikiem liczb
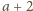 i
i
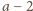 , to
, to
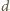 dzieli także różnicę tych liczb. Liczba
dzieli także różnicę tych liczb. Liczba
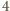 (poza liczbami
(poza liczbami
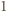 i
i
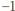 ) ma tylko parzyste dzielniki i dlatego liczby
) ma tylko parzyste dzielniki i dlatego liczby
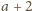 i
i
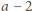 są względnie pierwsze. Wnioskujemy stąd, że
są względnie pierwsze. Wnioskujemy stąd, że
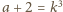 i
i
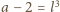 , gdzie
, gdzie
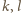 są liczbami nieparzystymi. Z definicji liczb
są liczbami nieparzystymi. Z definicji liczb
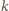 i
i
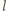 wiemy, że
wiemy, że
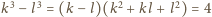 .
Zauważmy, że liczba
.
Zauważmy, że liczba
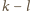 nie może być równa
nie może być równa
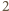 , ponieważ
liczba
, ponieważ
liczba
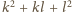 jest nieparzysta. Pozostał do rozważenia przypadek
jest nieparzysta. Pozostał do rozważenia przypadek
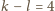 . Wtedy
. Wtedy
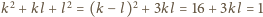 , co
prowadzi do równości
, co
prowadzi do równości
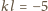 . Jedyne pary liczb całkowitych
. Jedyne pary liczb całkowitych
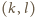 , gdzie
, gdzie
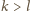 , spełniające tę równość, to
, spełniające tę równość, to
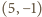 oraz
oraz
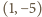 . W obu przypadkach
. W obu przypadkach
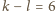 i otrzymujemy
sprzeczność, która kończy rozwiązanie zadania.
i otrzymujemy
sprzeczność, która kończy rozwiązanie zadania.