Określamy parę ciągów
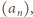
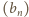 wzorami:
wzorami:
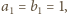
 | (1) |
Wówczas
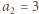 oraz
oraz
co pokazuje, że
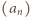 jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
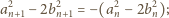
a ponieważ
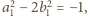 wynika stąd, że
wynika stąd, że
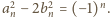
Określamy parę ciągów
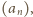
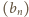 wzorami:
wzorami:
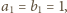
 | (2) |
Wówczas
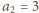 oraz
oraz
co pokazuje, że
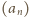 jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
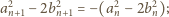
a ponieważ
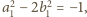 wynika stąd, że
wynika stąd, że
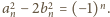
Ustalmy
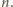 Widać, że
Widać, że
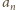 jest liczbą nieparzystą. Niech
jest liczbą nieparzystą. Niech
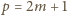 będzie jej dowolnym dzielnikiem pierwszym. Dostajemy
zależność
będzie jej dowolnym dzielnikiem pierwszym. Dostajemy
zależność
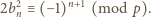
Po podniesieniu do potęgi
 (i skorzystaniu z małego twierdzenia
Fermata:
(i skorzystaniu z małego twierdzenia
Fermata:
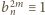 ),
),
 | (3) |
Za chwilę wykażemy, że
 | (4) |
Równość (mod
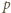 ) prawych stron (2) i (3) oznacza, że
) prawych stron (2) i (3) oznacza, że
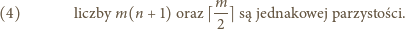
Dla
 parzystego warunek (4) mówi, że
parzystego warunek (4) mówi, że
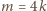 lub
lub
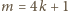 dla pewnego
dla pewnego
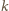 ; zatem
; zatem
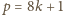 lub
lub
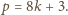 Każdy dzielnik pierwszy liczby
Każdy dzielnik pierwszy liczby
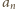 ma więc taką
postać. Dowolny dzielnik dodatni (jako iloczyn pewnej liczby dzielników
pierwszych) wtedy też jest tej postaci.
ma więc taką
postać. Dowolny dzielnik dodatni (jako iloczyn pewnej liczby dzielników
pierwszych) wtedy też jest tej postaci.
Dla
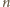 nieparzystego warunek (4) implikuje
nieparzystego warunek (4) implikuje
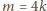 lub
lub
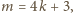 czyli
czyli
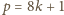 lub
lub
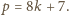 I znów, dowolny
iloczyn takich liczb też jest liczbą tej postaci. W obu przypadkach liczby postaci
I znów, dowolny
iloczyn takich liczb też jest liczbą tej postaci. W obu przypadkach liczby postaci
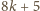 nie mogą być dzielnikami liczby
nie mogą być dzielnikami liczby
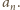
Pozostaje udowodnić wzór (3). Przyjmijmy (dla ustalonego
 )
oznaczenia:
)
oznaczenia:
Iloczyn
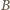 liczy
liczy
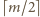 czynników. Łączymy je z czynnikami
iloczynu
czynników. Łączymy je z czynnikami
iloczynu
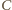 w pary o sumie
w pary o sumie
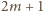 (czyli
(czyli
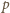 ). Otrzymujemy
związek
). Otrzymujemy
związek
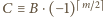 (mod
(mod
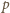 ). Stąd
). Stąd
Wystarczy teraz podzielić przez czynnik
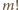 (względnie pierwszy z
(względnie pierwszy z
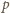 ), by uzyskać wzór (3) i zakończyć rozwiązanie.
), by uzyskać wzór (3) i zakończyć rozwiązanie.
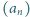 jest określony rekurencyjnie:
jest określony rekurencyjnie:
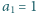 ,
,
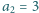 ,
,
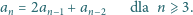
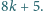

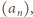
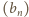 wzorami:
wzorami:
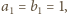

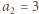 oraz
oraz
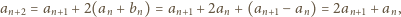
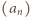 jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
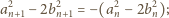
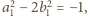 wynika stąd, że
wynika stąd, że
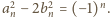
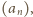
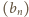 wzorami:
wzorami:
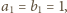

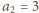 oraz
oraz
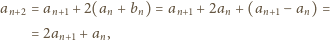
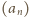 jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
jest ciągiem danym w zadaniu. Ze wzorów (1)
dostajemy równość
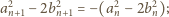
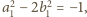 wynika stąd, że
wynika stąd, że
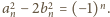
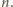 Widać, że
Widać, że
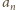 jest liczbą nieparzystą. Niech
jest liczbą nieparzystą. Niech
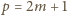 będzie jej dowolnym dzielnikiem pierwszym. Dostajemy
zależność
będzie jej dowolnym dzielnikiem pierwszym. Dostajemy
zależność
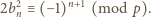
 (i skorzystaniu z małego twierdzenia
Fermata:
(i skorzystaniu z małego twierdzenia
Fermata:
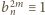 ),
),


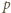 ) prawych stron (2) i (3) oznacza, że
) prawych stron (2) i (3) oznacza, że
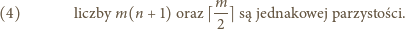
 parzystego warunek (4) mówi, że
parzystego warunek (4) mówi, że
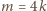 lub
lub
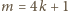 dla pewnego
dla pewnego
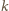 ; zatem
; zatem
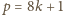 lub
lub
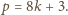 Każdy dzielnik pierwszy liczby
Każdy dzielnik pierwszy liczby
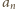 ma więc taką
postać. Dowolny dzielnik dodatni (jako iloczyn pewnej liczby dzielników
pierwszych) wtedy też jest tej postaci.
ma więc taką
postać. Dowolny dzielnik dodatni (jako iloczyn pewnej liczby dzielników
pierwszych) wtedy też jest tej postaci.
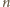 nieparzystego warunek (4) implikuje
nieparzystego warunek (4) implikuje
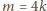 lub
lub
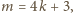 czyli
czyli
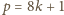 lub
lub
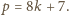 I znów, dowolny
iloczyn takich liczb też jest liczbą tej postaci. W obu przypadkach liczby postaci
I znów, dowolny
iloczyn takich liczb też jest liczbą tej postaci. W obu przypadkach liczby postaci
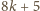 nie mogą być dzielnikami liczby
nie mogą być dzielnikami liczby
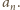
 )
oznaczenia:
)
oznaczenia:
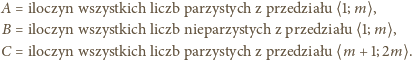
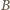 liczy
liczy
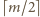 czynników. Łączymy je z czynnikami
iloczynu
czynników. Łączymy je z czynnikami
iloczynu
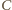 w pary o sumie
w pary o sumie
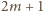 (czyli
(czyli
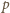 ). Otrzymujemy
związek
). Otrzymujemy
związek
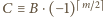 (mod
(mod
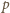 ). Stąd
). Stąd
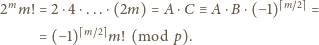
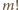 (względnie pierwszy z
(względnie pierwszy z
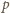 ), by uzyskać wzór (3) i zakończyć rozwiązanie.
), by uzyskać wzór (3) i zakończyć rozwiązanie.