Szukamy liczb całkowitych dodatnich
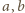 oraz liczby pierwszej
oraz liczby pierwszej
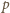 ,
dla których
,
dla których
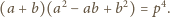
Dla
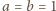 powyższe równanie sprowadza się do
powyższe równanie sprowadza się do
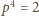 , co
spełnione być nie może. Przyjmijmy więc bez straty ogólności, że
, co
spełnione być nie może. Przyjmijmy więc bez straty ogólności, że
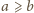 oraz
oraz
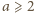 . Wtedy
. Wtedy
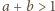 oraz
oraz
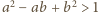 ,
skąd wniosek, że
,
skąd wniosek, że
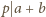 oraz
oraz
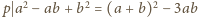 .
A zatem
.
A zatem
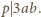 Wobec tego
Wobec tego
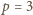 lub
lub
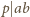 .
.
W przypadku, gdy
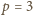 , otrzymujemy równanie
, otrzymujemy równanie
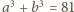 .
Bezpośrednio sprawdzamy, że równanie to nie ma rozwiązań w liczbach
całkowitych dodatnich
.
Bezpośrednio sprawdzamy, że równanie to nie ma rozwiązań w liczbach
całkowitych dodatnich
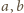 .
.
Z kolei z podzielności
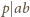 wynika, że
wynika, że
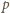 jest dzielnikiem
jednej z liczb
jest dzielnikiem
jednej z liczb
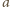 lub
lub
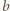 , co po wykorzystaniu podzielności
, co po wykorzystaniu podzielności
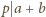 pozwala wywnioskować, że liczba
pozwala wywnioskować, że liczba
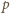 jest dzielnikiem obu
liczb
jest dzielnikiem obu
liczb
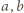 . Wobec tego
. Wobec tego
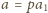 ,
,
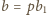 , gdzie liczby
, gdzie liczby
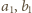 są całkowite i dodatnie. Dane równanie przybiera wtedy
postać
są całkowite i dodatnie. Dane równanie przybiera wtedy
postać
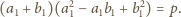
A ponieważ
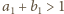 , więc
, więc
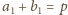 oraz
oraz
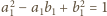 .
Z ostatniej równości dostajemy:
.
Z ostatniej równości dostajemy:
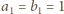 . Stąd
. Stąd
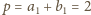 ,
,
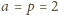 oraz
oraz
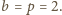
Bezpośrednie sprawdzenie dowodzi, że para
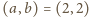 spełnia
warunki zadania.
spełnia
warunki zadania.
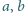 , dla których liczba
, dla których liczba
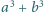 jest czwartą potęgą liczby pierwszej.
jest czwartą potęgą liczby pierwszej.