Zadanie ZM-K44-573
o zadaniu...
- Publikacja w Delcie: maj 2009
- Publikacja elektroniczna: 18 czerwca 2010
Dowieść, że dla każdej liczby naturalnej
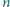 istnieje taki ciąg
arytmetyczny liczb naturalnych
istnieje taki ciąg
arytmetyczny liczb naturalnych
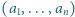 oraz taki ciąg geometryczny
liczb naturalnych
oraz taki ciąg geometryczny
liczb naturalnych
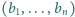 , że
, że


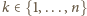 . Funkcja
. Funkcja
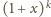 ma w punkcie
ma w punkcie
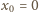 pochodną równą
pochodną równą
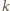 , więc jej iloraz różnicowy jest
mniejszy od
, więc jej iloraz różnicowy jest
mniejszy od
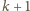 dla
dla
 bliskich
bliskich
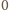 :
:
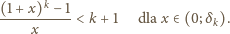
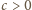 , mniejszą od liczb
, mniejszą od liczb
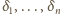 .
Wówczas
.
Wówczas
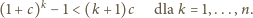

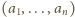 i
i
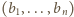 spełniają
postulowane warunki: zachodzą nierówności
spełniają
postulowane warunki: zachodzą nierówności
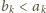 ; zaś zależności
; zaś zależności
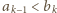 dla
dla
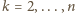 , czyli
, czyli
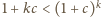 , to
nierówność Bernoulliego.
, to
nierówność Bernoulliego.