Zauważmy, że jeśli liczba
 jest żądanej postaci, to także
liczba
jest żądanej postaci, to także
liczba
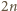 jest tej postaci. Ponadto
jest tej postaci. Ponadto
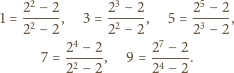
Stąd wynika, że każda z liczb
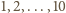 da się przedstawić
w żądanej postaci.
da się przedstawić
w żądanej postaci.
Wykażemy teraz, że nie istnieją liczby całkowite dodatnie
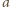 ,
,
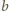 ,
,
 ,
,
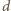 , dla których
, dla których
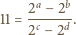
Bez straty ogólności możemy przyjąć, że
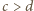 , wówczas
, wówczas
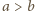 . Podstawiając
. Podstawiając
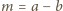 ,
,
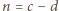 ,
,
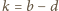 otrzymujemy zależność
otrzymujemy zależność

Stąd wynika, że
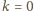 . Z kolei dla
. Z kolei dla
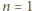 nie istnieje liczba
całkowita dodatnia
nie istnieje liczba
całkowita dodatnia
 spełniająca zależność
spełniająca zależność
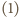 . A zatem
. A zatem
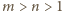 .Wówczas liczby
.Wówczas liczby
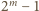 i
i
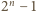 dają resztę
dają resztę
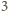 z dzielenia przez
z dzielenia przez
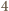 . Stąd obie strony zależności
. Stąd obie strony zależności
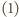 dają różne
reszty z dzielenia przez
dają różne
reszty z dzielenia przez
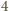 . Otrzymana sprzeczność dowodzi, że
liczby
. Otrzymana sprzeczność dowodzi, że
liczby
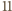 nie da się przedstawić w żądanej postaci.
nie da się przedstawić w żądanej postaci.

 ,
,
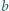 ,
,
 ,
,
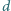 są liczbami całkowitymi dodatnimi.
są liczbami całkowitymi dodatnimi.