Zadanie ZM-1477
o zadaniu...
- Publikacja w Delcie: grudzień 2015
- Publikacja elektroniczna: 30-11-2015
Dany jest ciąg dodatnich liczb całkowitych 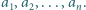 Ruch polega na wyborze dwóch takich indeksów
Ruch polega na wyborze dwóch takich indeksów 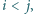 że
że 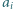 nie dzieli
nie dzieli 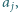 i zastąpieniu liczb
i zastąpieniu liczb 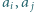 przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.

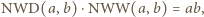 to iloczyn
to iloczyn 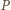 wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez
wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez 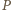 i ograniczony z dołu przez
i ograniczony z dołu przez 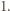 Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach
Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach 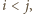 liczba
liczba 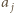 jest zamieniana na większą
jest zamieniana na większą 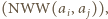 liczba
liczba 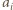 zaś - na mniejszą
zaś - na mniejszą 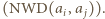 Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez
Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez 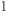 ) ani zwiększany (jako ograniczony z góry przez
) ani zwiększany (jako ograniczony z góry przez 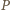 ). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów.
). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów.