Zadanie ZM-1461
o zadaniu...
- Publikacja w Delcie: czerwiec 2015
- Publikacja elektroniczna: 31-05-2015
Dana jest dodatnia liczba parzysta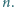 
W turnieju, w którym bierze udział 
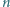drużyn, zostanie rozegranych 
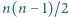meczów każdy z każdym. Wykazać, że możliwe jest takie podzielenie rozgrywek na 
rund, by każda drużyna wystąpiła w każdej rundzie dokładnie raz.
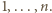Niech w 
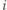-tej rundzie (dla 
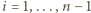) drużyny 
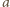i 
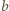(dla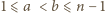 
) grają ze sobą, jeśli 
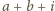jest podzielne przez 
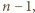zaś drużyny 
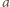i 
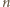(dla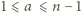 
) - jeśli 
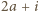jest podzielne przez 
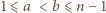dokładnie jedna spośród 
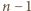kolejnych liczb 
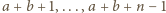jest podzielna przez 
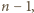więc 
i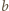 
zagrają ze sobą w dokładnie jednej z rund. Podobnie drużyny 
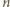i 
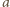dla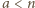 
zagrają ze sobą dokładnie raz, ponieważ dokładnie jedna z liczb 
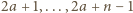jest podzielna przez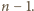 
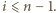Gdyby drużyna 
grała w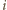 
-tej rundzie dwa razy, to dla pewnych 
liczba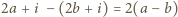 
byłaby podzielna przez 
Ponieważ 
jest parzyste, dostalibyśmy, że 
co jest niemożliwe. Gdyby drużyna 
grała dwa razy w 
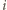-tej rundzie, to zachodziłaby jedna z dwóch możliwości: 1) drużyna 
gra z drużynami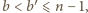 
skąd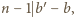 
a to jest niemożliwe; 2) drużyna 
gra z drużynami 
i 
skąd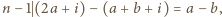 
co również jest niemożliwe.