Rozważmy takie losowanie par różnych komisji, że dla dowolnych dwóch par prawdopodobieństwo ich wylosowania jest jednakowe. Wylosujmy w ten sposób pewną parę komisji i oznaczmy przez 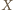 liczbę wspólnych członków tej pary. Niech
liczbę wspólnych członków tej pary. Niech 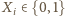 będzie funkcją charakterystyczną
będzie funkcją charakterystyczną 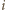 -tej osoby, czyli
-tej osoby, czyli 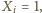 jeżeli
jeżeli 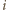 -ta osoba należy do obu wylosowanych komisji oraz
-ta osoba należy do obu wylosowanych komisji oraz 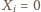 w przeciwnym przypadku. Funkcje
w przeciwnym przypadku. Funkcje 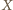 oraz
oraz 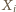 są zmiennymi losowymi. Ponieważ
są zmiennymi losowymi. Ponieważ 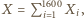 więc zachodzi równość
więc zachodzi równość ![|E[X]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/10x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba
Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba ![| E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/11x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) jest w rzeczywistości prawdopodobieństwem tego, że
jest w rzeczywistości prawdopodobieństwem tego, że 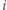 -ta osoba należy do obu z wylosowanych komisji. Jeśli przez
-ta osoba należy do obu z wylosowanych komisji. Jeśli przez 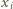 oznaczymy więc liczbę komisji, do których należy
oznaczymy więc liczbę komisji, do których należy 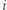 -ta osoba ze stowarzyszenia, to zachodzi równość
-ta osoba ze stowarzyszenia, to zachodzi równość
![E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/15x-081b9846768cfbd773023286d0e3f4b920dfc8c7-dm-66,57,43-FF,FF,FF.gif)
Skoro każda komisja zawiera 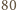 członków, to mamy ponadto
członków, to mamy ponadto 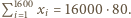 Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy
Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy
Zmienna losowa 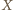 przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż
przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż 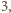 to co najmniej raz przyjmuje ona wartość nie mniejszą niż
to co najmniej raz przyjmuje ona wartość nie mniejszą niż 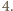 Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.
Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.
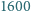 -osobowym stowarzyszeniu działa
-osobowym stowarzyszeniu działa 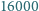 komisji, z których każda złożona jest z
komisji, z których każda złożona jest z 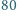 osób. Udowodnić, że pewne dwie różne komisje mają przynajmniej czterech wspólnych członków.
osób. Udowodnić, że pewne dwie różne komisje mają przynajmniej czterech wspólnych członków.
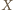 liczbę wspólnych członków tej pary. Niech
liczbę wspólnych członków tej pary. Niech 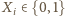 będzie funkcją charakterystyczną
będzie funkcją charakterystyczną 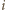 -tej osoby, czyli
-tej osoby, czyli 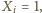 jeżeli
jeżeli 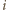 -ta osoba należy do obu wylosowanych komisji oraz
-ta osoba należy do obu wylosowanych komisji oraz 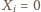 w przeciwnym przypadku. Funkcje
w przeciwnym przypadku. Funkcje 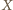 oraz
oraz 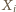 są zmiennymi losowymi. Ponieważ
są zmiennymi losowymi. Ponieważ 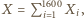 więc zachodzi równość
więc zachodzi równość ![|E[X]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/10x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba
Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba ![| E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/11x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) jest w rzeczywistości prawdopodobieństwem tego, że
jest w rzeczywistości prawdopodobieństwem tego, że 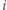 -ta osoba należy do obu z wylosowanych komisji. Jeśli przez
-ta osoba należy do obu z wylosowanych komisji. Jeśli przez 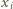 oznaczymy więc liczbę komisji, do których należy
oznaczymy więc liczbę komisji, do których należy 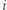 -ta osoba ze stowarzyszenia, to zachodzi równość
-ta osoba ze stowarzyszenia, to zachodzi równość![E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/15x-081b9846768cfbd773023286d0e3f4b920dfc8c7-dm-66,57,43-FF,FF,FF.gif)
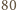 członków, to mamy ponadto
członków, to mamy ponadto 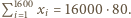 Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy
Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy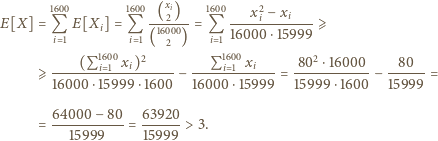
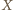 przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż
przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż 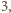 to co najmniej raz przyjmuje ona wartość nie mniejszą niż
to co najmniej raz przyjmuje ona wartość nie mniejszą niż 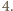 Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.
Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.