Wykażemy, że jeżeli każdy element zbioru 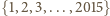 pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący
pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący 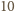 -wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem
-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem 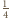 i że losowania są niezależne.
i że losowania są niezależne.
Ustalmy chwilowo pojedynczy 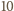 -wyrazowy ciąg arytmetyczny. Jest
-wyrazowy ciąg arytmetyczny. Jest 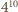 wszystkich możliwych pokolorowań tego ciągu, z których dokładnie
wszystkich możliwych pokolorowań tego ciągu, z których dokładnie 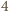 składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem
składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem 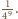 Oszacujmy od góry liczbę
Oszacujmy od góry liczbę 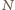 wszystkich rosnących
wszystkich rosnących 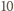 -wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy
-wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy 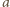 oraz różnicę
oraz różnicę 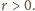 Spełnione są przy tym nierówności
Spełnione są przy tym nierówności 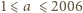 oraz
oraz 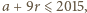 czyli
czyli 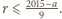 Dla ustalonego
Dla ustalonego  istnieje więc co najwyżej
istnieje więc co najwyżej 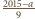 ciągów, których pierwszym wyrazem jest
ciągów, których pierwszym wyrazem jest 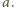 Otrzymujemy zatem nierówność
Otrzymujemy zatem nierówność
Ponumerujmy wszystkie 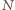 z rozważanych ciągów w sposób dowolny i dla
z rozważanych ciągów w sposób dowolny i dla 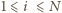 oznaczmy przez
oznaczmy przez 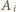 zdarzenie, w którym
zdarzenie, w którym 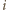 -ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas
-ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas
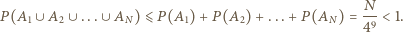
Prawdopodobieństwo zdarzenia, w którym pewien ciąg pomalowany został z użyciem wyłącznie jednego koloru, jest mniejsze niż 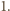 Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.
Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.
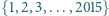 na jeden z czterech kolorów w taki sposób, że żaden rosnący 10-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze.
na jeden z czterech kolorów w taki sposób, że żaden rosnący 10-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze.
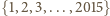 pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący
pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący 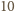 -wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem
-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem 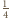 i że losowania są niezależne.
i że losowania są niezależne.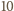 -wyrazowy ciąg arytmetyczny. Jest
-wyrazowy ciąg arytmetyczny. Jest 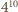 wszystkich możliwych pokolorowań tego ciągu, z których dokładnie
wszystkich możliwych pokolorowań tego ciągu, z których dokładnie 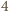 składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem
składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem 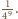 Oszacujmy od góry liczbę
Oszacujmy od góry liczbę 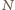 wszystkich rosnących
wszystkich rosnących 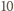 -wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy
-wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy 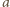 oraz różnicę
oraz różnicę 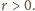 Spełnione są przy tym nierówności
Spełnione są przy tym nierówności 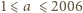 oraz
oraz 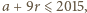 czyli
czyli 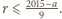 Dla ustalonego
Dla ustalonego  istnieje więc co najwyżej
istnieje więc co najwyżej 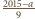 ciągów, których pierwszym wyrazem jest
ciągów, których pierwszym wyrazem jest 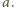 Otrzymujemy zatem nierówność
Otrzymujemy zatem nierówność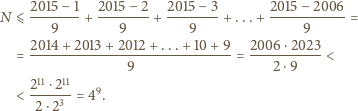
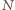 z rozważanych ciągów w sposób dowolny i dla
z rozważanych ciągów w sposób dowolny i dla 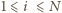 oznaczmy przez
oznaczmy przez 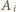 zdarzenie, w którym
zdarzenie, w którym 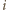 -ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas
-ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas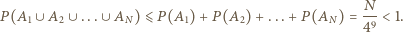
 Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.
Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.