Zadanie ZM-14.12-SEM-3
o zadaniu...
- Zadanie olimpijskie: LXV OM
- Publikacja w Delcie: grudzień 2014
- Publikacja elektroniczna: 01-12-2014
-
Rozwiązanie pochodzi od Adama Klukowskiego (Liceum im. S. Staszica w Warszawie).
Dane są względnie pierwsze liczby całkowite 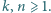 Na tablicy napisano w pewnej kolejności wszystkie dodatnie liczby całkowite nieprzekraczające
Na tablicy napisano w pewnej kolejności wszystkie dodatnie liczby całkowite nieprzekraczające 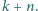 Ruch polega na zamianie miejscami dwóch liczb różniących się o
Ruch polega na zamianie miejscami dwóch liczb różniących się o 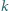 albo o
albo o 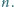 Dowieść, że można wykonać ciąg ruchów, który doprowadzi liczby na tablicy do kolejności
Dowieść, że można wykonać ciąg ruchów, który doprowadzi liczby na tablicy do kolejności 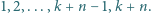

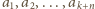 oznacza dany ciąg. Niech
oznacza dany ciąg. Niech 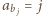 dla
dla 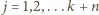 - ta równość definiuje jednoznacznie liczbę
- ta równość definiuje jednoznacznie liczbę 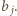 Dla ciągu
Dla ciągu 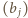 ruch polega na zamianie jego dwóch wyrazów znajdujących się w odległości
ruch polega na zamianie jego dwóch wyrazów znajdujących się w odległości 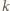 lub
lub 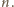 Jeśli umiemy posortować drugi ciąg, to pierwszy też. Definiujemy ciąg
Jeśli umiemy posortować drugi ciąg, to pierwszy też. Definiujemy ciąg 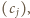 przyjmując, że
przyjmując, że 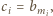 gdzie
gdzie 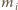 oznacza tę liczbę spośród
oznacza tę liczbę spośród 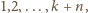 dla której różnica
dla której różnica 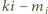 jest podzielna przez
jest podzielna przez 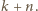 Ponieważ
Ponieważ 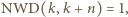 więc ciąg
więc ciąg 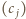 to permutacja ciągu
to permutacja ciągu 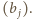 Ruchy w ciągu
Ruchy w ciągu 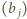 odpowiadają zamianie kolejnych wyrazów ciągu
odpowiadają zamianie kolejnych wyrazów ciągu 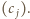 Do ciągu
Do ciągu 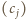 można zastosować sortowanie bąbelkowe pozwalające ustawić jego wyrazy w dowolnej kolejności.
można zastosować sortowanie bąbelkowe pozwalające ustawić jego wyrazy w dowolnej kolejności.