Zadanie ZM-1388
o zadaniu...
- Publikacja w Delcie: czerwiec 2013
- Publikacja elektroniczna: 28-05-2013
Król zaprosił na przyjęcie
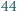rycerzy. Wiadomo, że każdy rycerz ma
wśród pozostałych co najwyżej
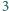wrogów (zakładamy, że jeśli
rycerz
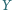jest wrogiem rycerza
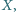to i
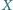jest wrogiem
rycerza
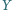). Udowodnić, że można tak rozsadzić rycerzy przy dwóch
stołach (dowolnie dużych), by każdy rycerz siedział przy stole z co najwyżej
jednym ze swoich wrogów.
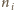oznacza liczbę wrogów
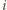-tego rycerza, którzy zasiadają
z nim przy stole. W kroku 0 posadźmy wszystkich rycerzy przy pierwszym
stole. Będziemy w kolejnych krokach przesadzać rycerzy, rozważając
liczbę
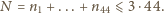
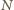zmienia się na
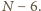Jeśli zaś
siedział on przy stole wraz z dwoma wrogami, to
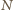zmienia się na
liczbę niewiększą niż
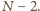Skoro po wykonaniu każdego kroku
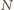maleje, to wykonamy ich skończenie wiele. Oczywiście, po
wykonaniu ostatniego kroku
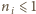dla każdego
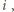co kończy
dowód.