Klub 44M - zadania XI 2012»Zadanie 650
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2012
- Publikacja w Delcie: listopad 2012
- Publikacja elektroniczna: 1 listopada 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (74 KB)
Zadanie 650 zostało opracowane na podstawie propozycji, którą zgłosił pan Paweł Kubit z Krakowa.
Dane są liczby naturalne
 oraz
oraz
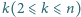 . Wyznaczyć
maksymalną liczbę wież, które można ustawić na szachownicy o rozmiarach
. Wyznaczyć
maksymalną liczbę wież, które można ustawić na szachownicy o rozmiarach
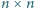 tak, by wśród dowolnie wybranych
tak, by wśród dowolnie wybranych
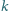 wież były dwie,
które się wzajemnie atakują (przyjmujemy, że atakują się wzajemnie każde
dwie wieże, stojące w tym samym rzędzie poziomym lub pionowym,
niezależnie od tego, czy są pomiędzy nimi jeszcze jakieś inne wieże).
wież były dwie,
które się wzajemnie atakują (przyjmujemy, że atakują się wzajemnie każde
dwie wieże, stojące w tym samym rzędzie poziomym lub pionowym,
niezależnie od tego, czy są pomiędzy nimi jeszcze jakieś inne wieże).

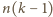 wież w żądany sposób; wystarczy
zapełnić nimi prostokąt
wież w żądany sposób; wystarczy
zapełnić nimi prostokąt
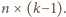 Pokażemy, że więcej się nie
da.
Pokażemy, że więcej się nie
da.
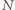 wież. Niech
wież. Niech
 będzie
największą liczbą wież, jakie można wybrać spośród nich, by żadne dwie
się nie atakowały. Należy dowieść, że jeśli
będzie
największą liczbą wież, jakie można wybrać spośród nich, by żadne dwie
się nie atakowały. Należy dowieść, że jeśli
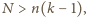 to
to
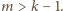 Wystarczy wykazać, że
Wystarczy wykazać, że
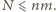
 wież, z których żadne dwie nie stoją w jednym
wierszu ani jednej kolumnie. Permutując wiersze i kolumny, można przyjąć,
że te wieże stoją na polach
wież, z których żadne dwie nie stoją w jednym
wierszu ani jednej kolumnie. Permutując wiersze i kolumny, można przyjąć,
że te wieże stoją na polach
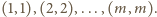 Podzielmy
szachownicę na cztery obszary
Podzielmy
szachownicę na cztery obszary
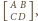 gdzie
gdzie
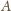 jest kwadratem
jest kwadratem
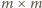 (na jego przekątnej stoją wybrane wieże),
(na jego przekątnej stoją wybrane wieże),
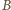 i
i
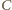 to
prostokąty
to
prostokąty
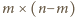 oraz
oraz
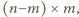 zaś
zaś
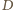 to kwadrat
to kwadrat
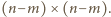 Wobec maksymalności
Wobec maksymalności
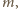 żadna wieża nie
znajduje się w obrębie kwadratu
żadna wieża nie
znajduje się w obrębie kwadratu
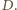
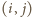 w prostokącie
w prostokącie
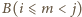 i symetryczne
do niego pole
i symetryczne
do niego pole
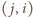 w prostokącie
w prostokącie
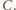 Gdyby na obu tych polach
stały wieże, to usuwając z poprzednio ustalonego układu wieżę z pola
Gdyby na obu tych polach
stały wieże, to usuwając z poprzednio ustalonego układu wieżę z pola
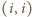 oraz dołączając wieże z pól
oraz dołączając wieże z pól
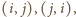 otrzymalibyśmy
układ
otrzymalibyśmy
układ
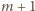 wież, stojących w różnych wierszach i kolumnach
– wbrew maksymalności
wież, stojących w różnych wierszach i kolumnach
– wbrew maksymalności
 Zatem co najwyżej połowa pól
w sumie prostokątów
Zatem co najwyżej połowa pól
w sumie prostokątów
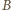 i
i
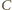 jest zajęta, czyli nie więcej
niż
jest zajęta, czyli nie więcej
niż
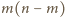 pól. Uwzględniając
pól. Uwzględniając
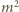 pól kwadratu
pól kwadratu
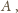 uzyskujemy oczekiwane oszacowanie:
uzyskujemy oczekiwane oszacowanie: