Podzielmy nasze
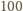 monet na trzy rozłączne podzbiory
monet na trzy rozłączne podzbiory
 ,
,
 i
i
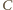 , mające odpowiednio 33, 33 i 34 elementy. Najpierw
ważymy zbiory
, mające odpowiednio 33, 33 i 34 elementy. Najpierw
ważymy zbiory
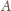 i
i
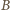 . Jeśli jeden, powiedzmy
. Jeśli jeden, powiedzmy
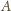 , jest
cięższy, to wiemy, że zawiera co najwyżej jedną fałszywą monetę. Wybieramy
wtedy z
, jest
cięższy, to wiemy, że zawiera co najwyżej jedną fałszywą monetę. Wybieramy
wtedy z
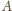 dwie monety i ważymy je. Wiadomo, że ta, która nie jest
lżejsza, jest prawdziwa. Jeśli jednak
dwie monety i ważymy je. Wiadomo, że ta, która nie jest
lżejsza, jest prawdziwa. Jeśli jednak
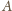 i
i
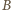 mają tę samą masę, to
mamy trzy przypadki:
mają tę samą masę, to
mamy trzy przypadki:
-
(a)
-
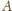 i
i
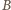 nie zawierają fałszywej monety,
nie zawierają fałszywej monety,
-
(b)
-
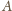 i
i
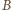 zawierają po jednej fałszywej monecie,
zawierają po jednej fałszywej monecie,
-
(c)
-
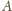 i
i
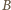 zawierają po dwie fałszywe monety.
zawierają po dwie fałszywe monety.
Wybieramy dowolną monetę
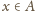 i ważymy zbiory
i ważymy zbiory
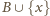 i
i
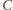 .
Jeśli mają równe masy, to musiał zajść przypadek (b), więc każda moneta
z
.
Jeśli mają równe masy, to musiał zajść przypadek (b), więc każda moneta
z
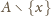 jest prawdziwa. Jeśli
jest prawdziwa. Jeśli
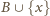 jest cięższy, to
nie mógł zajść przypadek (c), więc moneta
jest cięższy, to
nie mógł zajść przypadek (c), więc moneta
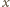 jest prawdziwa.
Wreszcie, jeśli
jest prawdziwa.
Wreszcie, jeśli
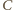 jest cięższy, to mamy przypadek (c), więc każda
moneta z
jest cięższy, to mamy przypadek (c), więc każda
moneta z
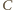 jest prawdziwa.
jest prawdziwa.
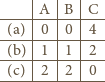
Tabelka pokazuje liczbę fałszywych monet w każdym ze zbiorów
w odpowiednim przypadku.
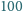 monet dokładnie
monet dokładnie
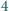 są fałszywe. Wszystkie prawdziwe
monety ważą tyle samo. Podobnie fałszywe. Wiadomo, że fałszywa moneta jest
lżejsza od prawdziwej. Jak znaleźć przynajmniej jedną prawdziwą monetę
za pomocą dwóch ważeń na wadze szalkowej?
są fałszywe. Wszystkie prawdziwe
monety ważą tyle samo. Podobnie fałszywe. Wiadomo, że fałszywa moneta jest
lżejsza od prawdziwej. Jak znaleźć przynajmniej jedną prawdziwą monetę
za pomocą dwóch ważeń na wadze szalkowej?

 monet na trzy rozłączne podzbiory
monet na trzy rozłączne podzbiory
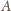 ,
,
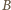 i
i
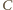 , mające odpowiednio 33, 33 i 34 elementy. Najpierw
ważymy zbiory
, mające odpowiednio 33, 33 i 34 elementy. Najpierw
ważymy zbiory
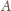 i
i
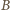 . Jeśli jeden, powiedzmy
. Jeśli jeden, powiedzmy
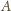 , jest
cięższy, to wiemy, że zawiera co najwyżej jedną fałszywą monetę. Wybieramy
wtedy z
, jest
cięższy, to wiemy, że zawiera co najwyżej jedną fałszywą monetę. Wybieramy
wtedy z
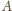 dwie monety i ważymy je. Wiadomo, że ta, która nie jest
lżejsza, jest prawdziwa. Jeśli jednak
dwie monety i ważymy je. Wiadomo, że ta, która nie jest
lżejsza, jest prawdziwa. Jeśli jednak
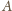 i
i
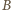 mają tę samą masę, to
mamy trzy przypadki:
mają tę samą masę, to
mamy trzy przypadki:
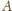 i
i
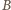 nie zawierają fałszywej monety,
nie zawierają fałszywej monety,
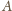 i
i
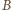 zawierają po jednej fałszywej monecie,
zawierają po jednej fałszywej monecie,
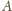 i
i
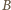 zawierają po dwie fałszywe monety.
zawierają po dwie fałszywe monety.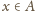 i ważymy zbiory
i ważymy zbiory
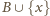 i
i
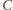 .
Jeśli mają równe masy, to musiał zajść przypadek (b), więc każda moneta
z
.
Jeśli mają równe masy, to musiał zajść przypadek (b), więc każda moneta
z
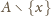 jest prawdziwa. Jeśli
jest prawdziwa. Jeśli
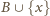 jest cięższy, to
nie mógł zajść przypadek (c), więc moneta
jest cięższy, to
nie mógł zajść przypadek (c), więc moneta
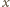 jest prawdziwa.
Wreszcie, jeśli
jest prawdziwa.
Wreszcie, jeśli
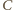 jest cięższy, to mamy przypadek (c), więc każda
moneta z
jest cięższy, to mamy przypadek (c), więc każda
moneta z
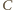 jest prawdziwa.
jest prawdziwa.