Zadanie ZM-1321
o zadaniu...
- Publikacja w Delcie: sierpień 2011
- Publikacja elektroniczna: 31-07-2011
Dane są: jeden klocek
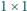i dwadzieścia jeden klocków
.
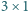Udowodnić, że tymi klockami można pokryć szachownicę
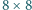(klocki
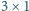można kłaść poziomo lub pionowo) wtedy i tylko
wtedy, gdy klocek
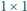położony jest na jednym z pól c3, f3, c6
lub f6.
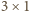przykrywa dokładnie jedno zamalowane pole. Tych
klocków jest 21, więc klocek
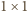musi leżeć na zamalowanym
polu. Wykonujemy symetryczne kolorowanie, ale innym kolorem niż
poprzednio, względem prostej zawierającej wspólny bok pól a4 i a5.
Widać już, że klocek
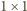musi leżeć na jednym z czterech pól
zamalowanych obydwoma kolorami, a to właśnie pola wymienione
w tezie zadania. Z drugiej strony łatwo sprawdzić, że jeśli leży on
na jednym z tych pól, to można skonstruować odpowiednie pokrycie
szachownicy.