Zadanie ZM-1317
o zadaniu...
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31-05-2011
W turnieju tenisa stołowego wzięło udział
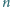 zawodników (
zawodników (
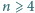 ).
Każdy zawodnik rozegrał dokładnie jeden mecz z każdym innym zawodnikiem,
żaden mecz nie zakończył się remisem. Po turnieju wszyscy zawodnicy usiedli
przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą
siedzącą obok niego z jego lewej strony. Wykaż, że istnieją tacy trzej
zawodnicy
).
Każdy zawodnik rozegrał dokładnie jeden mecz z każdym innym zawodnikiem,
żaden mecz nie zakończył się remisem. Po turnieju wszyscy zawodnicy usiedli
przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą
siedzącą obok niego z jego lewej strony. Wykaż, że istnieją tacy trzej
zawodnicy
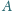 ,
,
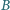 i
i
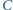 , że
, że
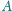 wygrał z
wygrał z
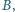
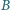 wygrał z
wygrał z
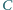 oraz
oraz
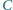 wygrał z
wygrał z
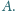

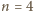 sprawa jest jasna. Załóżmy więc, że twierdzenie jest
prawdziwe dla pewnego
sprawa jest jasna. Załóżmy więc, że twierdzenie jest
prawdziwe dla pewnego
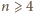 i spróbujmy je udowodnić dla
i spróbujmy je udowodnić dla
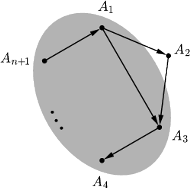
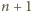 zawodników. Nazwijmy ich
zawodników. Nazwijmy ich
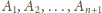 i przyjmijmy, że
w tej właśnie kolejności siedzą przy stole, czyli
i przyjmijmy, że
w tej właśnie kolejności siedzą przy stole, czyli
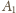 wygrał z
wygrał z
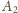 ,
który wygrał z
,
który wygrał z
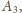 itd.
itd.
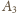 wygrał z
wygrał z
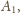 to mamy tezę. W przeciwnym
przypadku tezę otrzymujemy, stosując założenie indukcyjne do zawodników
to mamy tezę. W przeciwnym
przypadku tezę otrzymujemy, stosując założenie indukcyjne do zawodników