Jeśli w każdym wierszu jest permutacja liczb
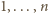 , to
, to
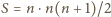 . Gdy w dokładnie jednym wierszu jest ciąg stały
. Gdy w dokładnie jednym wierszu jest ciąg stały
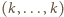 , a w każdym z pozostałych wierszy jest permutacja liczb
, a w każdym z pozostałych wierszy jest permutacja liczb
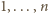 , wówczas
, wówczas
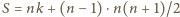 .
.
Gdy w dwóch wierszach są ciągi stałe
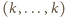 ,
,
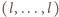 ,
przy czym
,
przy czym
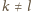 , to w każdej kolumnie musi być permutacja liczb
, to w każdej kolumnie musi być permutacja liczb
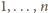 , i znów
, i znów
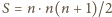 . Jeśli zaś
. Jeśli zaś
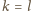 , to
w każdej kolumnie musi być ciąg stały
, to
w każdej kolumnie musi być ciąg stały
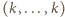 , więc
, więc
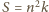 .
.
Reasumując, możliwymi wartościami sumy
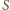 są liczby
są liczby
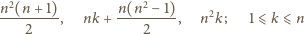
(i wszystkie one faktycznie mogą być osiągnięte) – razem, a priori,
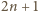 wartości. Czy jednak są one różne? Możliwe, że (dla pewnych
wartości. Czy jednak są one różne? Możliwe, że (dla pewnych
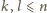 ) ma miejsce któraś z równości
) ma miejsce któraś z równości
Każde z równań (1) i (2) sprowadza się do
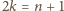 ; nie ma więc
rozwiązania, gdy
; nie ma więc
rozwiązania, gdy
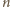 jest liczbą parzystą, ma natomiast dokładnie jedno
rozwiązanie
jest liczbą parzystą, ma natomiast dokładnie jedno
rozwiązanie
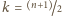 , gdy
, gdy
 jest liczbą nieparzystą. Równanie (3)
przekształcamy do postaci
jest liczbą nieparzystą. Równanie (3)
przekształcamy do postaci
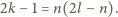
I znów: dla
 parzystego – brak rozwiązań. Dla
parzystego – brak rozwiązań. Dla
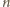 nieparzystego: lewa strona przedstawia liczbę mniejszą niż
nieparzystego: lewa strona przedstawia liczbę mniejszą niż
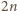 , prawa –
wielokrotność
, prawa –
wielokrotność
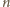 . Równość zachodzi jedynie, gdy obie strony są
równe
. Równość zachodzi jedynie, gdy obie strony są
równe
 , czyli dla
, czyli dla
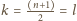 .
.
Wniosek: gdy
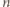 jest liczbą parzystą, wszystkie wyznaczone na początku
wartości są różne; suma
jest liczbą parzystą, wszystkie wyznaczone na początku
wartości są różne; suma
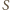 może mieć każdą z tych
może mieć każdą z tych
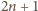 wartości. Gdy
wartości. Gdy
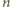 jest liczbą nieparzystą, wartość
jest liczbą nieparzystą, wartość
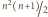 powtarza się trzykrotnie; jest więc
powtarza się trzykrotnie; jest więc
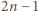 możliwych wartości
sumy
możliwych wartości
sumy
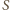 .
.
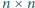 wpisujemy dodatnią
liczbę całkowitą niewiększą od
wpisujemy dodatnią
liczbę całkowitą niewiększą od
 tak, by w każdym wierszu oraz
w każdej kolumnie wszystkie liczby były równe lub wszystkie liczby
były różne. Niech
tak, by w każdym wierszu oraz
w każdej kolumnie wszystkie liczby były równe lub wszystkie liczby
były różne. Niech
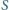 będzie sumą wszystkich liczb w tabelce.
Ile różnych wartości
będzie sumą wszystkich liczb w tabelce.
Ile różnych wartości
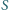 można w ten sposób uzyskać (dla
ustalonego
można w ten sposób uzyskać (dla
ustalonego
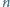 )?
)?

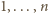 , to
, to
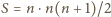 . Gdy w dokładnie jednym wierszu jest ciąg stały
. Gdy w dokładnie jednym wierszu jest ciąg stały
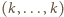 , a w każdym z pozostałych wierszy jest permutacja liczb
, a w każdym z pozostałych wierszy jest permutacja liczb
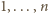 , wówczas
, wówczas
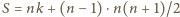 .
.
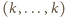 ,
,
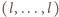 ,
przy czym
,
przy czym
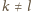 , to w każdej kolumnie musi być permutacja liczb
, to w każdej kolumnie musi być permutacja liczb
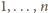 , i znów
, i znów
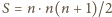 . Jeśli zaś
. Jeśli zaś
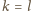 , to
w każdej kolumnie musi być ciąg stały
, to
w każdej kolumnie musi być ciąg stały
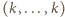 , więc
, więc
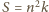 .
.
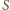 są liczby
są liczby
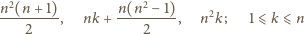
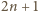 wartości. Czy jednak są one różne? Możliwe, że (dla pewnych
wartości. Czy jednak są one różne? Możliwe, że (dla pewnych
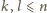 ) ma miejsce któraś z równości
) ma miejsce któraś z równości
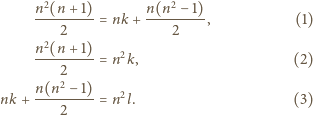
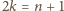 ; nie ma więc
rozwiązania, gdy
; nie ma więc
rozwiązania, gdy
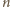 jest liczbą parzystą, ma natomiast dokładnie jedno
rozwiązanie
jest liczbą parzystą, ma natomiast dokładnie jedno
rozwiązanie
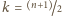 , gdy
, gdy
 jest liczbą nieparzystą. Równanie (3)
przekształcamy do postaci
jest liczbą nieparzystą. Równanie (3)
przekształcamy do postaci
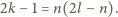
 parzystego – brak rozwiązań. Dla
parzystego – brak rozwiązań. Dla
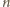 nieparzystego: lewa strona przedstawia liczbę mniejszą niż
nieparzystego: lewa strona przedstawia liczbę mniejszą niż
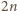 , prawa –
wielokrotność
, prawa –
wielokrotność
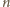 . Równość zachodzi jedynie, gdy obie strony są
równe
. Równość zachodzi jedynie, gdy obie strony są
równe
 , czyli dla
, czyli dla
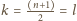 .
.
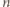 jest liczbą parzystą, wszystkie wyznaczone na początku
wartości są różne; suma
jest liczbą parzystą, wszystkie wyznaczone na początku
wartości są różne; suma
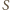 może mieć każdą z tych
może mieć każdą z tych
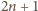 wartości. Gdy
wartości. Gdy
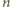 jest liczbą nieparzystą, wartość
jest liczbą nieparzystą, wartość
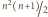 powtarza się trzykrotnie; jest więc
powtarza się trzykrotnie; jest więc
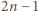 możliwych wartości
sumy
możliwych wartości
sumy
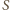 .
.