Łańcuch sfer»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Łańcuch sfer
- Publikacja w Delcie: czerwiec 2013
- Publikacja elektroniczna: 28-05-2013
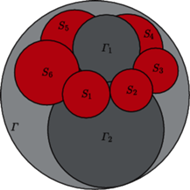
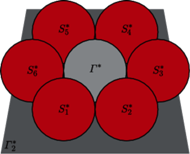
Szare sfery są parami styczne i każda z nich styczna jest do każdej z kolorowych sfer, tworzących łańcuch.
Styczne zewnętrznie sfery
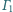 i
i
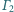 są styczne wewnętrznie do sfery
są styczne wewnętrznie do sfery
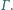 Do każdej z tych trzech sfer styczna jest każda z
Do każdej z tych trzech sfer styczna jest każda z
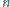 sfer
sfer
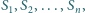 ponadto dla każdego
ponadto dla każdego
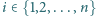 sfera
sfera
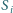 styczna jest do sfery
styczna jest do sfery
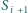 (przy czym
(przy czym
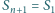 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch sfer
istnieje taki łańcuch sfer
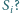 W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
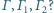 Czy i jak zależy to
od wyboru początkowej sfery
Czy i jak zależy to
od wyboru początkowej sfery
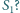

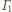 i
i
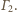 Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
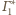 i
i
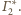 Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
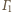 i
i
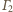 jest
środek inwersji.
jest
środek inwersji.
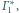
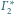
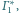
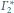
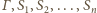 jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
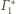 i
i
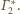 Z równoległości tych płaszczyzn wynika, że wszystkie sfery
Z równoległości tych płaszczyzn wynika, że wszystkie sfery
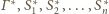 mają średnice równe odległości
mają średnice równe odległości
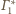 od
od
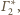 czyli są przystające. Ponadto wszystkie sfery
czyli są przystające. Ponadto wszystkie sfery
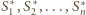 są
styczne do sfery
są
styczne do sfery
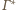 oraz dla każdego
oraz dla każdego
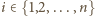 sfera
sfera
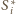 styczna jest do sfery
styczna jest do sfery
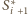 (przy czym
(przy czym
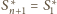 ).
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
).
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
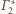 ) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
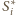 otacza środkową
piłeczkę
otacza środkową
piłeczkę
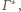 stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
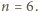
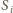 ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
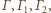 ani też od wyboru sfery
ani też od wyboru sfery
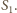 Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
 Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery
Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery