Załóżmy przeciwnie, że wielościan nie jest wpisany w sferę. 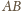Wtedy istnieją dwa wierzchołki wielościanu, dla których sfery z zadania ZM-1376 różnią się. Połączmy te wierzchołki ścieżką złożoną z krawędzi. 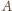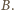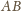Wtedy znajdziemy taką krawędź  na tej ścieżce, że sfera zawierająca wierzchołki ścian spotykających się w   różni się od sfery, w którą są wpisane ściany spotykające się w   Ale to znaczy, że dla sąsiednich ścian o wspólnej krawędzi  istnieją dwie różne sfery, w które te ściany są jednocześnie wpisane, co przeczy tezie zadania ZM-1375.