Zadanie ZM-1376
o zadaniu...
- Publikacja w Delcie: luty 2013
- Publikacja elektroniczna: 31-01-2013
Dany jest wielościan wypukły o następujących własnościach: w każdym wierzchołku spotykają się 3 krawędzie, każda ściana jest wielokątem wpisanym w okrąg.
Udowodnić, że trzy sąsiednie ściany są wpisane we wspólną sferę.


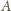 spotykają się trzy krawędzie, to w tym
wierzchołku spotykają się też trzy ściany. Oznaczmy je jak na rysunku.
spotykają się trzy krawędzie, to w tym
wierzchołku spotykają się też trzy ściany. Oznaczmy je jak na rysunku.
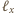 z płaszczyzną symetralną odcinka
z płaszczyzną symetralną odcinka
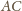 (przyjmujemy definicje i oznaczenia z rozwiązania zadania M
1375). Zauważmy, że należy on też do prostej
(przyjmujemy definicje i oznaczenia z rozwiązania zadania M
1375). Zauważmy, że należy on też do prostej
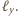 Istotnie,
należy do płaszczyzny symetralnej
Istotnie,
należy do płaszczyzny symetralnej
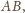 bo prosta
bo prosta
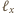 jest
w niej zawarta, i do płaszczyzny symetralnej
jest
w niej zawarta, i do płaszczyzny symetralnej
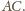 Przecięcie tych
płaszczyzn to właśnie prosta
Przecięcie tych
płaszczyzn to właśnie prosta
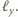 Podobnie, należy on do prostej
Podobnie, należy on do prostej
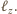 Jest więc równo odległy od wszystkich wierzchołków ścian
Jest więc równo odległy od wszystkich wierzchołków ścian