Zadanie ZM-1375
o zadaniu...
- Publikacja w Delcie: luty 2013
- Publikacja elektroniczna: 31-01-2013
Dany jest wielościan wypukły o następujących własnościach: w każdym wierzchołku spotykają się 3 krawędzie, każda ściana jest wielokątem wpisanym w okrąg.
Udowodnić, że każde dwie sąsiednie ściany są wpisane we wspólną, jednoznacznie wyznaczoną sferę.

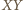 nazywamy płaszczyznę do niego
prostopadłą, przechodzącą przez jego środek.
nazywamy płaszczyznę do niego
prostopadłą, przechodzącą przez jego środek.
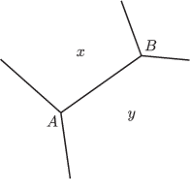
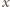 naszego wielościanu. Płaszczyzny
symetralne krawędzi tej ściany przecinają się wszystkie wzdłuż prostej
naszego wielościanu. Płaszczyzny
symetralne krawędzi tej ściany przecinają się wszystkie wzdłuż prostej
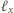 prostopadłej do ściany
prostopadłej do ściany
 i przechodzącej przez środek
okręgu opisanego na tej ścianie. Ta prosta jest zbiorem środków wszystkich
sfer zawierających wszystkie wierzchołki ściany
i przechodzącej przez środek
okręgu opisanego na tej ścianie. Ta prosta jest zbiorem środków wszystkich
sfer zawierających wszystkie wierzchołki ściany
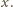
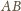 będzie wspólną krawędzią sąsiednich ścian
będzie wspólną krawędzią sąsiednich ścian
 i
i
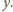 Proste
Proste
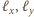 nie są równoległe i obie leżą
w płaszczyźnie symetralnej
nie są równoległe i obie leżą
w płaszczyźnie symetralnej
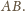 Przecinają się więc w jednym punkcie,
który jest środkiem sfery opisanej na ścianach
Przecinają się więc w jednym punkcie,
który jest środkiem sfery opisanej na ścianach
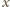 i
i
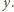
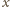 i
i
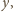 to
jej środek musi leżeć zarówno na prostej
to
jej środek musi leżeć zarówno na prostej
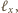 jak i na prostej
jak i na prostej
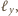 co dowodzi, że ta sfera jest wyznaczona jednoznacznie.
co dowodzi, że ta sfera jest wyznaczona jednoznacznie.