Inwersja w przestrzeni i rzut stereograficzny»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Inwersja w przestrzeni i rzut stereograficzny
- Publikacja w Delcie: grudzień 2012
- Publikacja elektroniczna: 30-11-2012
Wykazać, że dla dowolnego czworościanu istnieje trójkąt, którego boki są
równe co do wartości iloczynom przeciwległych krawędzi tego czworościanu.
Wykazać dodatkowo, że pole tego trójkąta jest równe
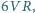 gdzie
gdzie
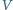 i
i
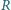 oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
