Inwersja w przestrzeni i rzut stereograficzny»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: OM 15-III-6
- Zadanie pochodzi z artykułu Inwersja w przestrzeni i rzut stereograficzny
- Publikacja w Delcie: grudzień 2012
- Publikacja elektroniczna: 30-11-2012
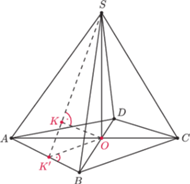
Dany jest ostrosłup
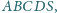 którego podstawą jest czworokąt wypukły
którego podstawą jest czworokąt wypukły
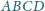 o prostopadłych przekątnych
o prostopadłych przekątnych
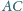 i
i
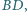 a rzutem
prostokątnym wierzchołka
a rzutem
prostokątnym wierzchołka
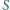 na podstawę jest punkt
na podstawę jest punkt
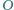 przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
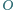 na
ściany boczne ostrosłupa leżą na jednym okręgu.
na
ściany boczne ostrosłupa leżą na jednym okręgu.

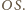 Weźmy rzut stereograficzny tej sfery z punktu
Weźmy rzut stereograficzny tej sfery z punktu
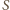 na
płaszczyznę
na
płaszczyznę
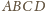 (
(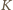 będzie rzutem prostokątnym
punktu
będzie rzutem prostokątnym
punktu
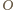 na ścianę
na ścianę
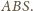 Płaszczyzna
Płaszczyzna
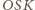 jest
prostopadła do krawędzi
jest
prostopadła do krawędzi
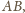 skąd wynika, że obraz
skąd wynika, że obraz
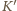 punktu
punktu
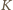 w tym przekształceniu będzie rzutem prostokątnym punktu
w tym przekształceniu będzie rzutem prostokątnym punktu
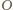 na krawędź
na krawędź
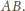 Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
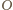 na pozostałe boki czworokąta
na pozostałe boki czworokąta
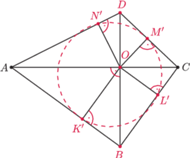
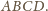 Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi –
Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi –