Inwersja w przestrzeni i rzut stereograficzny»Zadanie 1
o zadaniu...
- Zadanie olimpijskie: Rosja 2001
- Zadanie pochodzi z artykułu Inwersja w przestrzeni i rzut stereograficzny
- Publikacja w Delcie: grudzień 2012
- Publikacja elektroniczna: 30-11-2012
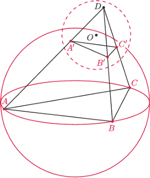
Sfera
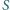 o środku w środku okręgu opisanego na trójkącie
o środku w środku okręgu opisanego na trójkącie
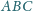 przecina krawędzie
przecina krawędzie
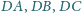 czworościanu
czworościanu
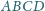 odpowiednio w punktach
odpowiednio w punktach
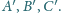 Płaszczyzny styczne
do tej sfery odpowiednio w punktach
Płaszczyzny styczne
do tej sfery odpowiednio w punktach
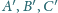 przecinają się w punkcie
przecinają się w punkcie
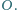 Wykazać, że punkt
Wykazać, że punkt
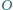 jest środkiem sfery opisanej na
czworościanie
jest środkiem sfery opisanej na
czworościanie
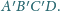

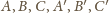 i sfera
opisana na czworościanie
i sfera
opisana na czworościanie
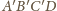 są prostopadłe. Zauważmy,
że
są prostopadłe. Zauważmy,
że
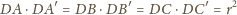
 Rozważmy inwersję o środku
Rozważmy inwersję o środku
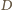 i promieniu
i promieniu
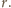 Zauważmy, że sfera
Zauważmy, że sfera
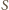 przechodzi na siebie, a punkty
przechodzi na siebie, a punkty
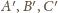 odpowiednio na
odpowiednio na
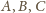 (i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
(i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
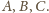 Jednakże środek sfery
Jednakże środek sfery
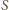 leży właśnie na
płaszczyźnie
leży właśnie na
płaszczyźnie
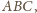 skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
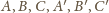 i sfera opisana na
czworościanie
i sfera opisana na
czworościanie
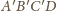 też są prostopadłe.
też są prostopadłe.