Wykażemy, że takie cztery punkty istnieją w każdym czworościanie.

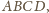Rozważmy dowolny czworościan  w którym 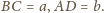 Na krawędziach 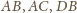 i 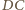  wybierzmy odpowiednio takie punkty 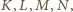 że

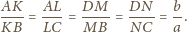
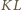Z twierdzenia odwrotnego do twierdzenia Talesa wynika, że proste  i 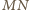  są równoległe. Wobec tego punkty 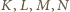 leżą na jednej płaszczyźnie. Ponadto z twierdzenia Talesa obliczamy

skąd

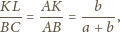
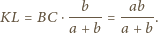
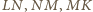Analogicznie wykazujemy, że każdy z odcinków  ma długość 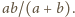 Stąd wniosek, że czworokąt 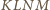 jest rombem.

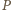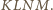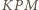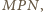Niech  będzie środkiem rombu  Punkty przecięcia prostych, zawierających dwusieczne kątów  i   z bokami rombu tworzą wierzchołki czworokąta. Czworokąt ten jest kwadratem, gdyż jego przekątne są równe i przecinają się pod kątem prostym.