Najmocniejsze twierdzenie stereometrii»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Najmocniejsze twierdzenie stereometrii
- Publikacja w Delcie: marzec 2010
- Publikacja elektroniczna: 18-06-2010
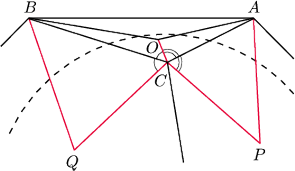
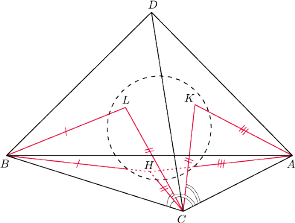
Sfera wpisana w czworościan
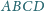 jest styczna do ściany
jest styczna do ściany
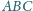 w punkcie
w punkcie
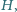 a sfera dopisana do tego czworościanu jest styczna do
ściany
a sfera dopisana do tego czworościanu jest styczna do
ściany
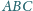 w punkcie
w punkcie
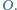 Dowieść, że jeżeli
Dowieść, że jeżeli
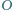 jest
środkiem okręgu opisanego na trójkącie
jest
środkiem okręgu opisanego na trójkącie
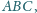 to
to
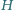 jest punktem
przecięcia wysokości tego trójkąta.
jest punktem
przecięcia wysokości tego trójkąta.

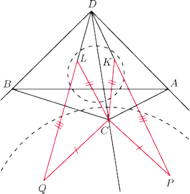
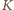 i
i
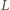 będą punktami styczności sfery wpisanej
w czworościan
będą punktami styczności sfery wpisanej
w czworościan
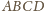 odpowiednio ze ścianami
odpowiednio ze ścianami
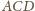 i
i
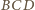 , a
, a
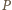 i
i
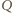 punktami styczności sfery dopisanej
odpowiednio z płaszczyznami
punktami styczności sfery dopisanej
odpowiednio z płaszczyznami
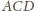 i
i
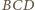 . Wówczas
trójkąty
. Wówczas
trójkąty
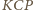 i
i
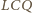 są przystające (
są przystające (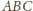 przy wierzchołkach
przy wierzchołkach
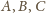 odpowiednio przez
odpowiednio przez
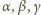 . Trójkąty
. Trójkąty
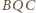 i
i
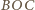 są
przystające, skąd wynika, że
są
przystające, skąd wynika, że
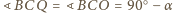 (
(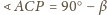 . Niech
. Niech
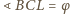 . Wtedy
. Wtedy
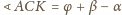 (bo
(bo
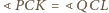 ). Jednakże
). Jednakże
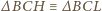 i
i
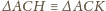 , więc
, więc
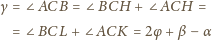
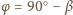 . Zatem
. Zatem
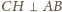 . Analogicznie
dowodzimy, że
. Analogicznie
dowodzimy, że
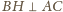 , a to oznacza, że
, a to oznacza, że
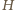 jest punktem
przecięcia wysokości trójkąta
jest punktem
przecięcia wysokości trójkąta
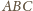 .
.