Zadanie

Narzędzia
Obiekty: Wielokąty
Słowa kluczowe
Kategoria: Planimetria

O deltoidach»Zadanie 6

o zadaniu...

Zadanie pochodzi z artykułu O deltoidach
Publikacja w Delcie: styczeń 2019
Publikacja elektroniczna: 31 grudnia 2018
Artykuł źródłowy w wersji do druku [application/pdf]: (432 KB)

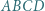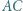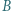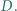Stół do bilarda ma kształt deltoidu $ABCD$ o osi symetrii $AC |$ i kątach prostych przy $|B$ i $. D$ Bila wybita z wierzchołka 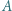$A$ po odbiciu od boku 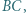$|BC,$ a następnie od 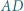$AD |$ trafia w wierzchołek 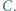$C.$ Wykaż, że środek drogi bili leży na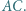 $AC.$

Wskazówka

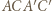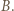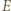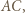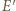Warto rozważyć romb $ACA|$ o środku w punkcie $B.$ Oznaczmy przez $|E$ punkt przecięcia drogi bili z odcinkiem $|AC,$ niech $E | ′$ będzie obrazem 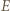$E$ w symetrii względem 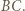$|BC.$ Wystarczy dowieść, że 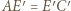$|AE$ i że odcinki te są równe rozprostowanym odpowiednim fragmentom drogi bili. Przyda się fakt, iż kąt padania bili równy jest kątowi odbicia.